

Nguyễn Việt Khoa
Giới thiệu về bản thân



































a) Các số tự nhiên có hai chữ số nhỏ hơn 200 là: {10;11;…;199}10; 11; …; 199 .
Vậy có 190 cách viết ngẫu nhiên một số tự nhiên có hai chữ số nhỏ hơn 200.
b) Có 9 kết quả thuận lợi cho biến cố“Số tự nhiên được viết ra là số tròn trăm” là 100;200;300;400;500;600;700;800;900.100 ; 200 ; 300 ; 400 ; 500 ; 600 ; 700 ; 800 ; 900.
Do đó, xác suất của biến cố “Số tự nhiên được viết ra là số tròn trăm” là: 91909190 .
Vì BD là đường phân giác của góc ABC nên:
ADDC=ABBC���� = ���� (t/chất đường phân giác)
Suy ra: ADAD+DC=ABAB+BC����+�� = ����+ �� hay ADAC=ABAB+BC���� = ����+ ��
Mà ΔABC cân tại A nên AC = AB = 15 (cm)
Suy ra: AD15=1515+10⇒AD=15.1515+10=9��15=1515+10⇒��=15.1515+10=9(cm)
Vậy DC = AC – AD = 15 – 9 = 6 (cm)
b) Vì BE ⊥ BD nên BE là đường phân giác góc ngoài tại đỉnh B
Suy ra : ECEA=BCBA���� =����( t/chất đường phân giác)
Suy ra: ECEC+CA=BCBA����+�� = ���� ⇒ EC.BA= BC (EC + AC)
Suy ra: EC.BA - EC.BC = BC.AC ⇒EC (BA - BC) = BC.AC
Vậy EC=BC.ACBA−BC=10.1515−10=30(cm)��= ��.����− �� = 10.1515−10 =30(��) .
M=x2+y2−xy−x+y+1�=�2+�2−��−�+�+1
4M=4x2+4y2−4xy−4x+4y+44�=4�2+4�2−4��−4�+4�+4
4M=(2x−y−1)2+3y2+2y+34�=(2�−�−1)2+3�2+2�+3
12M=3(2x−y−1)2+9y2+6y+912�=3(2�−�−1)2+9�2+6�+9
12M=(2x−y−1)2+(3y+1)2+812�=(2�−�−1)2+(3�+1)2+8
M≥13�≥13
⎧⎪
⎪⎨⎪
⎪⎩3y+1=0;y=−132x+13−1=0;x=−13
a) Xét Δ ABC có NA = NB; MA = MC
⇒ NM là đường trung bình của ΔABC
⇒ MN // BC; MN = 1/2 BC (1)
Xét Δ GBC có: DG = DB; EG = EC
⇒ ED là đường trung bình của Δ GBC
⇒ ED // BC; ED = 1/2 BC
Từ (1) và (2) suy ra: MN // DE; MN = ED
⇒ Tứ giác NMED là hình bình hành
⇒ ME // ND
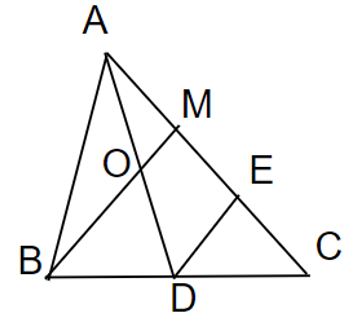
a/ Gọi E là trung điểm của MC
Từ giả thiết: AM=12MC��=12�� nên AM = ME = EC
Xét tam giác BCM có ME = EC (cmt); DB = DC (gt)
⇒ DE là đường trung bình của tam giác BCM
⇒ DE // BM
Xét tam giác ADE có
AM = ME (cmt)
BM // DE (cmt)
⇒ OM // DE
⇒ OA = OD (trong tam giác đường thẳng đi qua trung điểm của 1 cạnh và // với 1 cạnh thì đi qua trung điểm cạnh còn lại)
b/ Ta có DE là đường trung bình của tam giác BCM ⇒ DE=12BM��=12��
Xét tam giác ADE có
OA=OD (cmt); AM=ME (cmt) ⇒ OM là đường trung bình của tam giác ADE
⇒ OM=12DE=12.12BM=14BM��=12��=12.12��=14��.
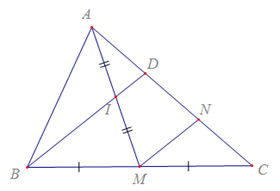
a) Qua M kẻ MN // BD.
Trong ΔAMN����, có I là trung điểm của AM, ID∥MN⇒AD=DN��∥��⇒��=��.
Trong ΔBCD����, có M là trung điểm của BC, MN∥BD⇒ND=NC��∥��⇒��=��.
⇒AD=DN=NC⇒AD=12DC⇒��=��=��⇒��=12��.
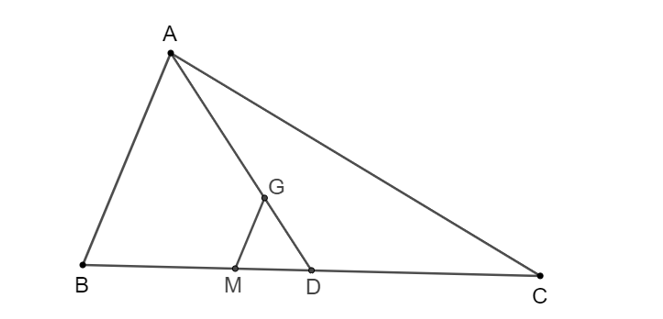
Lấy D là trung điểm của cạnh BC.
Khi đó, AD là đường trung tuyến của tam giác ABC.
Vì G là trọng tâm của tam giác ABC nên điểm G nằm trên cạnh AD.
Ta có AGAD=23����=23 hay AG=23AD��=23��.
Vì MG // AB, theo định lí Thalès, ta suy ra: AGAD=BMBD=23����=����=23.
Ta có BD = CD (vì D là trung điểm của cạnh BC) nên BMBC=BM2BD=22.3=13����=��2��=22 . 3=13.
Do đó BM=13BC��=13�� (đpcm).
Trong ΔADB, ta có: MN // AB (gt)
Suy ra: hệ quả định lí ta-lét) (1)
Trong ΔACB, ta có: PQ // AB (gt)
Suy ra: 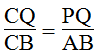
Lại có: NQ // AB (gt)
AB // CD (gt)
Suy ra: NQ // CD
Trong ΔBDC, ta có: NQ // CD (chứng minh trên)
Suy ra: 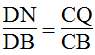
Từ (1), (2) và (3) suy ra 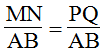
Xét tam giác ABC có BC ⊥ AB' và B'C'⊥ AB' nên suy ra BC // B'C'.
Theo hệ quả định lí Thalès, ta có:
ABAB′=BCBC′⇒xx+h=aa′⇒a′x=a(x+h)⇒a′x−ax=ah����'=����'⇒��+ℎ=��'⇒�'�=�(�+ℎ)⇒�'�−��=�ℎ
⇒x(a′−a)=ah⇒x=aha′−a⇒��'−�=�ℎ⇒�=�ℎ�'−� (đpcm)
Ta có: AB // CD (gt), áp dụng hệ quả của định lý Ta – lét ta có:
Suy ra (hệ quả định lí ta-lét)
Vậy OA.OD = OB.OC