Ta có: \(B = \left(\left[\right. z - \frac{3}{2} \left(\right. x + y \left.\right) \left]\right.\right)^{2} + \frac{3}{4} \left(\left(\right. x + \frac{y}{3} - \frac{4}{3} \left.\right)\right)^{2} + \frac{2}{3} \left(\right. y - 2 \left.\right)^{2} + 1 \geq 1\)

Vậy giá trị nhỏ nhất của \(B\) là \(1\) 

y−2=0
{ x+3y​−34​=0

z−23​(x+y)=0​

hay \(x = - \frac{2}{3}\); \(y = 2\); \(z = 4\).

​

a) Có \(2\) kết quả thuận lợi cho biến cố "Mặt xuất hiện của xúc xắc có số chấm là hợp số" là 4; 6.

Xác suất của biến cố đó là: \(\frac{2}{6} = \frac{1}{3}\).

b) Có \(2\) kết quả thuận lợi cho biến cố "Mặt xuất hiện của xúc xắc có số chấm là số chia hết cho 3 dư 2" là 2; 5.

Xác suất của biến cố đó là: \(\frac{2}{6} = \frac{1}{3}\).

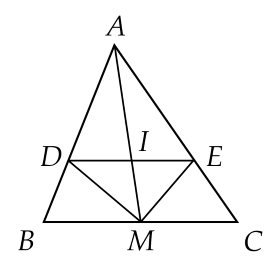
a) Theo tính chất đường phân giác ta có \(\frac{D A}{D B} = \frac{M A}{M B}\) và \(\frac{E A}{E C} = \frac{M A}{M C}\).

Mặt khác \(M B = M C\) nên \(\frac{D A}{D B} = \frac{E A}{E C}\).

Theo định lí Thalès đảo ta được \(D E\) // \(B C\).

b) Theo câu a ta có \(D E\) // \(B C\) nên \(\frac{A D}{A B} = \frac{A E}{A C}\).

Xét định lí Thalès cho \(\Delta A B M\) và \(\Delta \&\text{nbsp}; A C M\) ta có

\(\frac{A D}{A B} = \frac{D I}{B M}\) và \(\frac{A E}{A C} = \frac{I E}{C M}\).

Từ đó, suy ra \(\frac{D I}{B M} = \frac{I E}{C M}\) mà \(M B = C M\) nên \(D I = I E\) hay \(I\) là trung điểm của \(D E\).

a) Quảng cáo không hợp lí vì chỉ có 13 khách hàng chọn nhãn hiệu điện thoại Oppo trong tổng số 100 khách hàng mua điện thoại di động.

b) Quảng cáo không hợp lí vì chỉ có 13 khách hàng chọn nhãn hiệu điện thoại Oppo ít hơn nhãn hiệu Iphone và Samsung.

a) Xác suất thực nghiệm của biến cố "Mặt xuất hiện của xúc xắc là mặt 4 chấm" là \(\frac{22}{40}=\frac{11}{20}\).

b) Xác suất thực nghiệm của biến cố "Mặt xuất hiện của xúc xắc là mặt 6 chấm" là \(\frac{18}{40}=\frac{9}{20}\).

c) Xác suất thực nghiệm của biến cố "Mặt xuất hiện của xúc xắc là mặt 1 chấm" là \(\frac{14}{40}=\frac{7}{20}\).

d) Xác suất thực nghiệm của biến cố "Mặt xuất hiện của xúc xắc là mặt 3 chấm" là \(\frac{14}{20}=\frac{7}{10}\).

a) Qua \(D\) vẽ một đường thẳng song song với \(B M\) cắt \(A C\) tại \(N\).

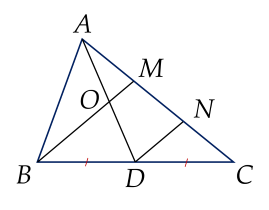
Xét \(\Delta M B C\) có \(D B = D C\) và \(D N\) // \(B M\) nên \(M N = N C = \frac{1}{2} M C\) (định lí đường trung bình của tam giác).

Mặt khác \(A M = \frac{1}{2} M C\), do đó \(A M = M N = \frac{1}{2} M C\).

Xét \(\Delta A N D\) có \(A M = M N\) và \(B M\) // \(D N\) nên \(O A = O D\) hay \(O\) là trung điểm của \(A D\).

b) Xét \(\Delta A N D\) có \(O M\) là đường trung bình nên \(O M = \frac{1}{2} D N\) (1) 

Xét \(\Delta M B C\) có \(D N\) là đường trung bình nên \(D N = \frac{1}{2} B M\). (2)

Từ (1) và (2) ta có \(O M = \frac{1}{4} B M\).

D(x)=2(x2−x)+(3y2−2y)+(4z2−2z)+2

\(= 2 \left(\right. x^{2} - x + \frac{1}{4} \left.\right) + 3 \left(\right. y^{2} - \frac{2}{3} y + \frac{1}{9} \left.\right) + \left[\right. \left(\right. 2 z \left.\right)^{2} - 2 z + \frac{1}{4} \left]\right. + 2 - \frac{1}{2} - \frac{1}{3} - \frac{1}{4}\)

\(= 2 \left(\left(\right. \left(\right. x - \frac{1}{2} \left.\right) \left.\right)\right)^{2} + 3 \left(\left(\right. \left(\right. y - \frac{1}{3} \left.\right) \left.\right)\right)^{2} + \left(\left(\right. \left(\right. 2 z - \frac{1}{2} \left.\right) \left.\right)\right)^{2} + \frac{11}{2} \geq \frac{11}{2}\)

Vậy giá trị nhỏ nhất của \(D\) là: \(\frac{11}{2}\) tại \(\left(\right. x , y , z \left.\right) = \left(\right. \frac{1}{2} ; \frac{1}{3} ; \frac{1}{4} \left.\right)\).

a) Tổng số học sinh của lớp là: 40.

Số học sinh Tốt chiếm số phần trăm là:

     16 : 40 . 100% = 40%

Số học sinh Khá chiếm số phần trăm là:

     11 : 40 . 100% = 27,5%

b) Số học sinh xếp loại Chưa đạt chiếm số phần trăm là:

     3 : 40 . 100% = 7,5%

Cô giáo thông báo tỉ lệ học sinh xếp loại Chưa đạt của lớp chiếm trên 7% là đúng.