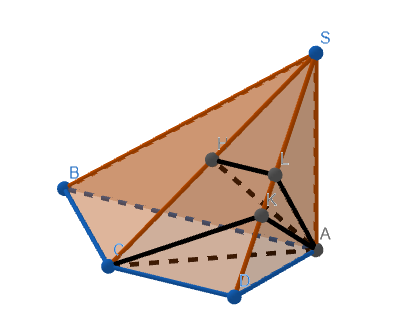
(1) (*) Vì \(SA\perp\left(ABCD\right)\) nên \(\widehat{SB,\left(ABCD\right)}=\widehat{SBA}=arctan\left(\dfrac{SA}{AB}\right)\) \(=arctan\left(\dfrac{a\sqrt{2}}{2a}\right)=arctan\left(\dfrac{\sqrt{2}}{2}\right)\approx35,26^o\)

(*) Ta có \(AC=AD\sqrt{2}=a\sqrt{2}\)  \(\Rightarrow AC=AS\) 

\(\Rightarrow\widehat{SC,\left(ABCD\right)}=\widehat{SCA}=45^o\) (tam giác ACS vuông cân tại A)

(2) (*) Qua H kẻ đường thẳng song song với DC cắt SD tại L. 

Ta có \(SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\) và \(CD\perp DA\)

\(\Rightarrow CD\perp\left(SAD\right)\)

Mà HL//CD \(\Rightarrow HL\perp\left(SAD\right)\)

\(\Rightarrow\widehat{AH,\left(ABCD\right)}=\widehat{HAL}=arcsin\left(\dfrac{HL}{HA}\right)\) \(=arcsin\left(\dfrac{\dfrac{CD}{2}}{\dfrac{SC}{2}}\right)\) \(=arcsin\left(\dfrac{CD}{SC}\right)\) \(=arcsin\left(\dfrac{a}{2a}\right)=arcsin\left(\dfrac{1}{2}\right)=30^o\)

(*) Có \(\dfrac{1}{AK^2}=\dfrac{1}{AD^2}+\dfrac{1}{AS^2}\Rightarrow AK=\dfrac{AD.AS}{\sqrt{AD^2+AS^2}}=\dfrac{a.a\sqrt{2}}{\sqrt{a^2+\left(a\sqrt{2}\right)^2}}=\dfrac{a\sqrt{6}}{3}\)

Có \(CD\perp\left(SAD\right)\Rightarrow CD\perp AK\)

Mà \(AK\perp SD\Rightarrow AK\perp\left(SCD\right)\)

\(\Rightarrow\widehat{AC,\left(SCD\right)}=\widehat{ACK}=arcsin\left(\dfrac{AK}{AC}\right)=arcsin\left(\dfrac{\dfrac{a\sqrt{6}}{3}}{a\sqrt{2}}\right)\) \(=arcsin\left(\dfrac{\sqrt{3}}{3}\right)\) \(\approx35,26^o\)

(3) Ta có \(CB^2+CA^2=\left(a\sqrt{2}\right)^2+\left(a\sqrt{2}\right)^2=4a^2=AB^2\) nên tam giác ABC vuông tại C

 \(\Rightarrow CA\perp CB\)

 Mà \(SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\)

\(\Rightarrow BC\perp\left(SAC\right)\)

\(\Rightarrow\widehat{SB,\left(SAC\right)}=\widehat{BSC}=arctan\left(\dfrac{BC}{CS}\right)=arctan\left(\dfrac{a\sqrt{2}}{2a}\right)\) \(=arctan\left(\dfrac{\sqrt{2}}{2}\right)\approx35,26^o\)

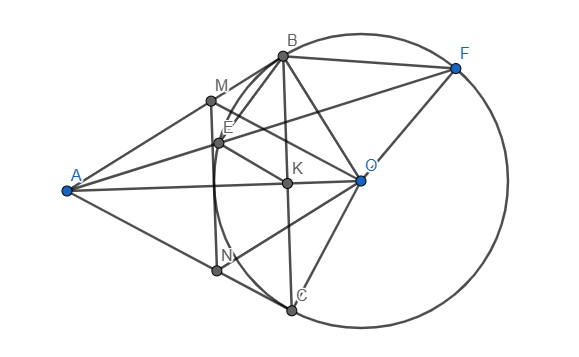
d) Trong đường tròn (O), có \(\widehat{ABE}\) , \(\widehat{AFB}\) lần lượt là góc tạo bởi tiếp tuyến và dây cung AB và góc nội tiếp chắn cung đó nên \(\widehat{ABE}=\widehat{AFB}\)

 \(\Delta ABE\) và \(\Delta AFB\) có \(\widehat{ABE}=\widehat{AFB}\left(cmt\right);\widehat{BAE}\equiv\widehat{BAF}\) 

 \(\Rightarrow\Delta ABE\sim\Delta AFB\left(g.g\right)\) \(\Rightarrow\dfrac{AB}{AF}=\dfrac{AE}{AB}\Rightarrow AB^2=AE.AF\)

 \(\Delta ABO\) vuông tại B có đường cao AK \(\Rightarrow AB^2=AK.AO\)

 Từ đó \(\Rightarrow AE.AF=AK.AO\) \(\Rightarrow\dfrac{AE}{AO}=\dfrac{AK}{AF}\)

 \(\Delta AEK\) và \(\Delta AOF\) có \(\dfrac{AE}{AO}=\dfrac{AK}{AF}\left(cmt\right);\widehat{EAK}\equiv\widehat{OAF}\)

 \(\Rightarrow\Delta AEK\sim\Delta AOF\left(c.g.c\right)\) \(\Rightarrow\widehat{AKE}=\widehat{OFA}\), ta có đpcm.

Ta có \(\sqrt{2+2\cos2x}=\sqrt{2+2\left(2\cos^2x-1\right)}=\sqrt{4\cos^2x}=2\left|\cos x\right|\)

\(\Leftrightarrow f\left(x\right)+f\left(-x\right)=2\left|\cos x\right|,\forall x\inℝ\)  (1)

Đặt \(g\left(x\right)=f\left(x\right)-\left|\cos x\right|\)

Khi đó (1) \(\Leftrightarrow\left[f\left(x\right)-\left|\cos x\right|\right]+\left[f\left(-x\right)-\left|\cos x\right|\right]=0\)

\(\Leftrightarrow g\left(x\right)+\left[f\left(-x\right)-\left|\cos\left(-x\right)\right|\right]=0\) (do \(\cos x\) là hàm chẵn)

\(\Leftrightarrow g\left(x\right)+g\left(-x\right)=0\)

\(\Leftrightarrow g\left(x\right)=-g\left(-x\right)\)

\(\Leftrightarrow g\left(x\right)\) là hàm lẻ

Khi đó \(f\left(x\right)=g\left(x\right)+\left|\cos x\right|\) với \(g\left(x\right)\) là hàm lẻ. Thử lại, ta thấy:

(1) \(\Leftrightarrow f\left(x\right)+f\left(-x\right)=g\left(x\right)+\left|\cos x\right|+g\left(-x\right)+\left|\cos\left(-x\right)\right|\)

\(\Leftrightarrow f\left(x\right)+f\left(-x\right)=2\left|\cos x\right|\), thỏa mãn

 Vậy \(f\left(x\right)=g\left(x\right)+\left|\cos x\right|\) với \(g\left(x\right)\) là hàm lẻ bất kì có tập xác định là \(ℝ\)

 \(\Rightarrow I=\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}f\left(x\right)dx\)

 \(I=\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}\left[g\left(x\right)+\left|\cos x\right|\right]dx\)

\(I=\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}g\left(x\right)dx+\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}\left|\cos x\right|dx\)

\(I=\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}\left|\cos x\right|dx\) (do \(g\left(x\right)\) là hàm lẻ)

\(I=\int\limits^{-\dfrac{\pi}{2}}_{-\dfrac{3\pi}{2}}\left(-\cos x\right)dx+\int\limits^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}\cos xdx+\int\limits^{\dfrac{3\pi}{2}}_{\dfrac{\pi}{2}}\left(-\cos x\right)dx\)

\(I=-\sin x|^{-\dfrac{\pi}{2}}_{-\dfrac{3\pi}{2}}+\sin x|^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}-\sin x|^{\dfrac{3\pi}{2}}_{\dfrac{\pi}{2}}\)

\(I=6\)

PTHH: \(CH_4+2O_2\underrightarrow{t^o}CO_2+2H_2O\)

Ta có \(n_{CH_4}=\dfrac{V_{CH_4}}{24,79}=\dfrac{12,395}{24,79}=0,5\left(mol\right)\)

\(\Rightarrow n_{O_2}=1\left(mol\right)\)

\(\Rightarrow V_{O_2}=n_{O_2}.24,79=24,79\left(l\right)\)

 Mình nghĩ chiếc nhẫn chỉ có \(10cm^3\) thôi chứ làm sao mà \(10m^3\) được.

 Giả sử chiếc vòng được làm hoàn toàn bằng vàng \(\Rightarrow m_{vòng}=D_{vàng}.V_{vòng}=19,3.10=193\left(g\right)\)

 Khối lượng bị thừa ra là \(193-171=22\left(g\right)\)

 Cứ thay \(1cm^3\) vàng bằng \(1cm^3\) bạc thì khối lượng chiếc vòng giảm đi \(8,9g\) \(\Rightarrow\) Thể tích bạc là \(\dfrac{22}{8,9}=\dfrac{220}{89}\left(cm^3\right)\)

 \(\Rightarrow\) Thể tích vàng là \(10-\dfrac{220}{89}=\dfrac{670}{89}\left(cm^3\right)\)

 Vậy thể tích vàng và bạc sử dụng làm chiếc nhẫn lần lượt là \(\dfrac{670}{89}cm^3\) và \(\dfrac{220}{89}cm^3\) 

\(\overline{abcd}⋮3\) \(\Rightarrow a+b+c+d⋮3\)

Xét biểu thức \(P=\left(a^3+b^3+c^3+d^3\right)-\left(a+b+c+d\right)\)

\(P=\left(a^3-a\right)+\left(b^3-b\right)+\left(c^3-c\right)+\left(d^3-d\right)\)

Xét số \(N=n^3-n\) với \(n\inℕ\). Ta có:

\(N=n\left(n^2-1\right)\)

\(N=n\left(n-1\right)\left(n+1\right)\)

Ta thấy N là tích của 3 số nguyên liên tiếp \(\Rightarrow N⋮3\)

\(\Rightarrow N=n^3-n⋮3,\forall n\inℕ\)

\(\Rightarrow P⋮3\)

hay \(\left(a^3+b^3+c^3+d^3\right)-\left(a+b+c+d\right)⋮3\)

Mà \(a+b+c+d⋮3\left(cmt\right)\) \(\Rightarrow a^3+b^3+c^3+d^3⋮3\), ta có đpcm.

Gọi \(u_n\) là số tiền Stacy có được sau lần thứ \(n\) \(\left(n\inℕ\right)\)

Khi đó dãy số \(\left(u_n\right)_{n\ge0}\) được xác định như sau:

\(\left\{{}\begin{matrix}u_0=X\\u_{n+1}=2u_n-1024,\forall n\ge0\end{matrix}\right.\) với X chính là số tiền ban đầu của Stacy.

Giả sử ta có \(u_{n+1}-a=b\left(u_n-a\right)\)

\(\Leftrightarrow u_{n+1}=bu_n+a-ab\)

Khi đó ta có \(\left\{{}\begin{matrix}b=2\\a-ab=-1024\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=2\\a=1024\end{matrix}\right.\)

\(\Rightarrow u_{n+1}-1024=2\left(u_n-1024\right)\)  

hay \(u_n-1024=2\left(u_{n-1}-1024\right)=2^2\left(u_{n-2}-1024\right)=...=2^n\left(u_0-1024\right)=2^n\left(X-2024\right)\) \(\Rightarrow u_n=2^n\left(X-1024\right)+1024\)

Sau lần thứ 10, Stacy hết sạch tiền, vậy ta có:

\(u_{10}=2^{10}\left(X-1024\right)+1024=0\)

\(\Leftrightarrow1024\left(X-1024\right)+1024=0\)

\(\Leftrightarrow X-1024+1=0\)

\(\Leftrightarrow X=1023\)

Vậy số tiền tối thiểu Stacy có ban đầu là 1023 đôla.

\(N=2n^3+3n^2+25n\)

\(=n\left(2n^2+3n+25\right)\)

Nếu \(n\) chẵn thì hiển nhiên \(N⋮2\)

Nếu \(n\) lẻ thì \(2n^2⋮2,\) 3n lẻ và 25 lẻ nên \(2n^2+3n+25\) chẵn \(\Rightarrow N⋮2\)

Vậy \(N⋮2\)

Nếu \(n⋮3\) thì hiển nhiên \(N⋮3\)

Nếu n chia 3 dư 1 thì \(2n^2+3n+25\equiv2.1^2+3.1+25\equiv30\equiv0\left(mod3\right)\) nên \(N⋮3\)

Nếu n chia 3 dư 2 thì \(2n^2+3n+25\equiv2.2^2+3.2+25\equiv39\equiv0\left(mod3\right)\) nên \(N⋮3\)

Vậy \(N⋮3\)

Ta có \(N⋮2,N⋮3\) và \(ƯCLN\left(2,3\right)=1\)

\(\Rightarrow N⋮6\)