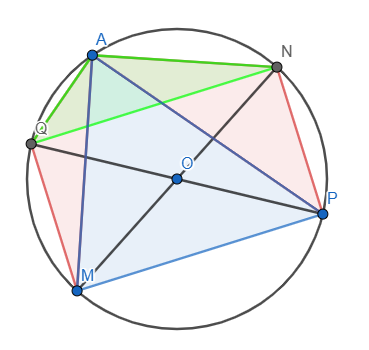
Trong hình trên, điểm A cố định và 2 đường kính MN, PQ thay đổi. Với mỗi cặp đường kính, điểm B có thể nằm ở M hoặc N, điểm C có thể nằm ở P và Q. Do đó có tất cả \(2^2=4\) cách chọn vị trí B và C. Tuy nhiên, chỉ khi B và C lần lượt nằm ở M và P thì tam giác ABC mới chứa O nên xác suất là \(\dfrac{1}{4}\).

 Trước hết, ta xét phiên bản 2D của bài toán này như sau:

 Bài toán: Lấy 3 điểm A, B, C bất kì nằm trên đường tròn (O). Tính xác suất để O nằm trong tam giác ABC.

 Giải: Cố định điểm A. Hai đường kính bất kì khác nhau của (O) cắt đường tròn tại 4 vị trí. Khi đó sẽ có 2 cách chọn điểm B và C trong 4 giao điểm, tức là sẽ có \(2^2=4\) cách khác nhau để "đặt" 2 điểm B, C.

 Trong 4 vị trí thì chỉ có 1 vị trí thỏa mãn tam giác ABC chứa O. Vì 3 điểm A, B, C đều xuất hiện ở các vị trí khác nhau trên đường tròn vớ khả năng như nhau nên xác suất để tam giác ABC chứa O là \(\dfrac{1}{4}\).

 Trở lại bài toán, ta cũng lập luận tương tự: Cố định một điểm. Khi đó 3 đường kính bất kỳ của mặt cầu cắt mặt cầu tại 6 điểm. Khi đó mỗi 1 trong 3 điểm còn lại đều có 2 cách chọn nên có tất cả \(2^3=8\) cách chọn 3 điểm. Trong 8 cách chọn thì chỉ có 1 cách thỏa mãn tứ diện ABCD chứa tâm mặt cầu. Do khả năng xuất hiện của 4 điểm ở tất cả các vị trí trên mặt cầu là như nhau nên xác suất để tâm hình cầu nằm trong tứ diện bằng \(\dfrac{1}{8}\).

 Vậy xác suất để tâm mặt cầu nằm trong tứ diện là \(\dfrac{1}{8}\).

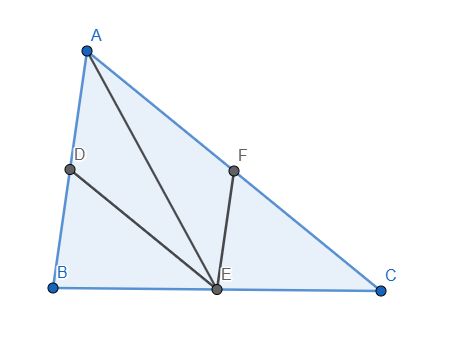
 Ta thấy DE là đường trung bình của tam giác ABC nên \(\left\{{}\begin{matrix}DE//AC\\DE=\dfrac{1}{2}AC\end{matrix}\right.\) hay \(\left\{{}\begin{matrix}DE//AF\\DE=AF\end{matrix}\right.\)

 Rõ ràng AE, AD, DE là 3 cạnh của tam giác ADE nên AE, AD, AF cũng là 3 cạnh của một tam giác. Ta có đpcm.

 Đặt \(P=\left(a+b\right)\left(b+c\right)\left(c+a\right)\)

 Trước tiên ta sẽ chứng minh \(P\) chẵn.

 Ta thấy rằng một số nguyên thì hoặc là số chẵn, hoặc là số lẻ. Tuy nhiên, ta có tới 3 số nguyên a, b, c. Điều này có nghĩa là sẽ tồn tại ít nhất 2 số trong 3 số a, b, c có cùng tính chẵn lẻ (nguyên lý Dirichlet). Khi đó tổng của 2 số này là một số chẵn \(\Rightarrow\) P chẵn.

 Ta chứng minh \(P⋮3\)

 Nếu trong 3 số a, b, c có ít nhất một số chia hết cho 3, không mất tính tổng quát, giả sử số đó là a. Khi đó vì \(a,abc,a+b+c+abc\) đều chia hết cho 3 nên \(b+c⋮3\) \(\Rightarrow P⋮3\)

 Nếu trong 3 số a, b, c không có số nào chia hết cho 3 thì sẽ có 2 trường hợp:

 TH1: Cả 3 số này khi chia cho 3 có cùng số dư.

  Khi đó \(a+b+c⋮3\) trong khi \(abc⋮̸3\Rightarrow a+b+c+abc⋮̸3\), không thỏa mãn.

 TH2: 3 số a, b, c chia cho 3 không có cùng số dư. Khi đó tồn tại một số chia 3 dư 1 và một số chia 3 dư 2. Tổng của 2 số này sẽ chia hết cho 3 \(\Rightarrow P⋮3\)

 Vậy \(P⋮3\)

 Ta có \(P⋮2,P⋮3\) và \(ƯCLN\left(2,3\right)=1\) nên \(P⋮6\). Ta có đpcm.

\(a\) \(\Rightarrow b+c⋮3\)

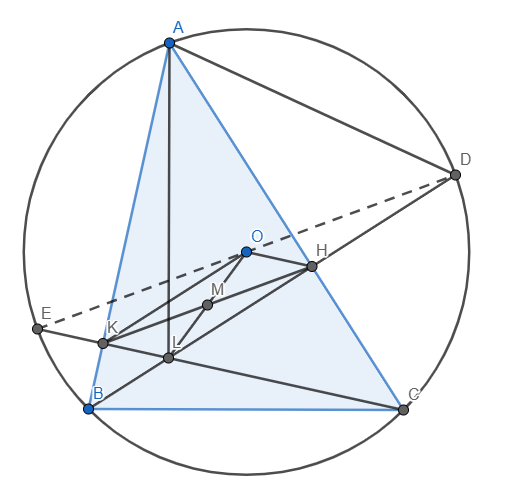
Gọi L là trực tâm tam giác ABC và M là trung điểm HK.

Tam giác HAB vuông tại H có \(\widehat{HAB}=45^o\Rightarrow\Delta HAB\) vuông cân tại H

\(\Rightarrow HA=HB\) \(\Rightarrow\) H thuộc đường trung trực của AB

Mà O là tâm đường tròn ngoại tiếp tam giác ABC \(\Rightarrow\) O cũng nằm trên trung trực của AB

\(\Rightarrow\) OH là đường trung trực của đoạn AB.

\(\Rightarrow OH\perp AB\)

Mà \(LK\perp AB\) (do L là trực tâm tam giác ABC) nên OH//LK

Tương tự, ta chứng minh được OK//LH 

\(\Rightarrow\) Tứ giác OHKL là hình bình hành.

Mà M là trung điểm HK \(\Rightarrow\) M cũng là trung điểm OL

Mặt khác, ta có \(\widehat{HAL}=\widehat{HBC}\) (cùng phụ với \(\widehat{ACB}\)) và \(\widehat{HBC}=\widehat{DBC}=\widehat{DAC}=\widehat{HAD}\) nên \(\widehat{HAL}=\widehat{HAD}\)

\(\Rightarrow\) AH là tia phân giác của \(\widehat{DAL}\). 

Lại có \(AH\perp DL\Rightarrow\Delta DAL\) cân tại A

\(\Rightarrow\) Đường cao AH cũng là trung tuyến \(\Rightarrow\) H là trung điểm DL

Do đó MH là đường trung bình của tam giác LOD

\(\Rightarrow\) MH//OD hay OD//HK

Tương tự, ta cũng chứng minh được OE//KH

\(\Rightarrow\) D, O, E thẳng hàng (tiên đề Euclid)

Ta có đpcm.

Mình lộn, không phải 68^oF đâu. Dùng công thức \(^oF=1,8\times^oC+32\) thì giả sử \(^oC_{TPHCM}-^oC_{ĐL}=10\left(^oC\right)\) thì

 \(^oF_{TPHCM}-^oF_{ĐL}=1,8\times\left(^oC_{TPHCM}-^oC_{ĐL}\right)=1,8\times10=18\left(^oF\right)\)

 Vậy chênh lệch theo thang Farenheit là 18^oF

Ta có công thức chuyển đổi từ độ C sang độ F:

\(^oF=1,8\times^oC+32\)

Do đó nếu chênh lệch nhiệt độ giữa Đà Lạt - TPHCM là 20^oC thì chênh lệch này theo thang Farenheit là \(1,8.20+32=68\left(^oF\right)\)

 Ta thấy \(x^2\) khi chia cho 4 chỉ có thể dư 0 hoặc 1 (tính chất của số chính phương) \(\Rightarrow x^2=4k+1\left(k\inℕ\right)\) hoặc \(x^2=4m\left(m\inℕ\right)\)

 Nếu \(x^2=4m\) thì \(7x^2-16y=25\) thành \(7.4m-16y=25\)

 Ta thấy vế trái chia hết cho 4 trong khi vế phải không chia hết cho 4 \(\Rightarrow\) vô lý

 Nếu \(x^2=4k+1\) thì \(7x^2-16y=25\) thành \(7\left(4k+1\right)-16y=25\) hay \(28k+7-16y=25\) 

 Ta thấy vế trái chia 4 dư 3 trong khi vế phải chia 4 dư 1 \(\Rightarrow\) vô lý

 Vậy không tồn tại số nguyên \(x,y\) nào thỏa mãn yêu cầu đề bài. Ta có đpcm.