

Lê Hồng Minh
Giới thiệu về bản thân



































h
Xét ΔPMNΔPMN có ABAB // MNMN (gt)
Suy ra ABMN=APPMMNAB=PMAP (hệ quả định lí Thalès).
Thay số: ABMN=APAP+AM=33+4=37⇒MN7=AB3MNAB=AP+AMAP=3+43=73⇒7MN=3AB.
Áp dụng tính chất dãy tỉ số bằng nhau: MN7=AB3=MN−AB7−3=84=27MN=3AB=7−3MN−AB=48=2
Suy ra MN=2.7=14MN=2.7=14 cm; AB=2.3=6AB=2.3=6 cm.
Vậy MN=14MN=14 cm; AB=6AB=6 cm.
2
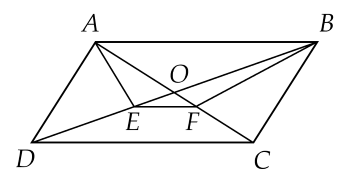
a) Xét Δ ADBΔ ADB có AEAE là phân giác trong của đỉnh AA (gt) suy ra BEED=ABADEDBE=ADAB (tính chất đường phân giác của tam giác).
Xét ΔBACΔBAC có BFBF là phân giác trong của đỉnh BB (gt) suy ra FAFC=ABBCFCFA=BCAB (tính chất đường phân giác của tam giác)
Thêm nữa AD=BCAD=BC (do ABCDABCD là hình bình hành) suy ra BEED=FAFCEDBE=FCFA.
Vậy ta có điều phải chứng minh.
b) Từ câu a ta có: BEED=FAFCEDBE=FCFA suy ra BE+EDED=FA+FCFCEDBE+ED=FCFA+FC
⇒DBED=ACFC⇒2ODED=2OCFC⇒ODED=OCFC⇒EDDB=FCAC⇒ED2OD=FC2OC⇒EDOD=FCOC
Xét ΔODCΔODC có: ODED=OCFCEDOD=FCOC (cmt) suy ra EFEF // CDCD (định lí Thalès đảo)
Vậy ta có điều phải chứng minh.
skibii
Fe