

Lê Vân Anh
Giới thiệu về bản thân



































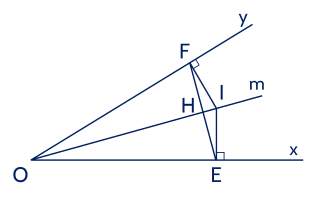
a) Xét tam giác IOE và tam giác IOF
Có góc E = góc F = 90 độ (gt)
OI chung
Góc EOI = góc FOI (gt)
=> Tam giác IOE = tam giác IOF (g.c.g)
b) Có tam giác IOE = tam giác IOF (cma)
=> OE=OF (2 cạnh tương ứng)
Mà H là giao điểm của Om và EF
=> EF vuông góc Om

a) Xét tam giác OAD và tam giác CBO
Có OA=OC (gt)
Góc O chung
OD=OB (gt)
=> Tam giác OAD = tam giác CBO (c.g.c)
=> AB=CD (2 cạnh tương ứng)
b) Do OC=OA; OD=OB nên AB=CD
Mà tam giác OAD = tam giác CBO (cma)
=> Góc OCB = góc ODA; góc CAD = góc OCB (2 góc tương ứng)
Xét tam giác ABE và tam giác CDE
Có góc OAD = góc OCB (cmt)
AB=CD (cmt)
Góc ABE = góc CDE (cmt)
=> Tam giác ABE = tam giác CDE (g.c.g)
c) Có tam giác ABE = tam giác CDE (cmb) nên AE=CE (2 cạnh tương ứng)
Xét tam giác CEO và tam giác AEO
Có AE=CE (cmt)
OE chung
OA=OC (cmt)
=> Tam giác CEO và tam giác AEO (c.c.c)
Mà tam giác CEO = tam giác AEO (cmt)
=> OE là tia phân giác góc xOy

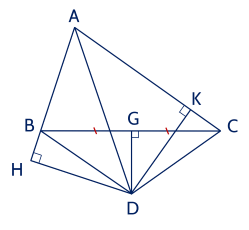
Xét tam giác BGD và tam giác CGD
Có góc BGD = góc CGD = 90 độ (DG là trung trực của BC)
BG=CG (gt)
DG chung
=> Tam giác BGD = tam giác CGD (2 cạnh góc vuông)
=> BD=CD (2 cạnh tương ứng)
Xét tam giác BHD và tam giác CKD
Có góc BHD = góc CKD = 90 độ (gt)
DH=DK (cmt)
BD=CD (cmt)
=> Tam giác BHD và tam giác CKD (chcgv)
=> BH=CK (cmt)


 a) Ta có BF = 2BE => BE = EF Mà BE = 2ED nên EF = 2ED => D laf trung điểm của EF => CD là đường trung tuyến của tam giác EFC. Vì K là trung điểm của CF nên EK là đường trung tuyến của tam giác EFC. Tam giác EFC có hai đường trung tuyến CD và EK cắt nhau tại G nên G là trọng tâm của tam giác EFC. b) Ta có G là trọng tâm của tam giác EFC nên GC/DC = 2/3 và GE = 2/3 EK. => GK = 1/3 EK => GE = 2GK => GE/GK = 2
a) Ta có BF = 2BE => BE = EF Mà BE = 2ED nên EF = 2ED => D laf trung điểm của EF => CD là đường trung tuyến của tam giác EFC. Vì K là trung điểm của CF nên EK là đường trung tuyến của tam giác EFC. Tam giác EFC có hai đường trung tuyến CD và EK cắt nhau tại G nên G là trọng tâm của tam giác EFC. b) Ta có G là trọng tâm của tam giác EFC nên GC/DC = 2/3 và GE = 2/3 EK. => GK = 1/3 EK => GE = 2GK => GE/GK = 2
 a) Ta có DM = DG => GM = 2GD. Ta lại có G laf giao điểm của BD và CE => G là trọng tâm của tam giác ABC. => BG = 2GD. => BG = GM. Chứng minh tương tự ta được CG = GN. b)Xét tam giác GMN và tam giác GBC. Có GM = GB (cmt). Góc GMN = góc BGC (2 góc đối đỉnh). GN = GC (cmt). => Tam giác GMN = tam giác GBC ( c.g.c). => MN = BC (2 cạnh tương ứng). Theo chứng minh trên tam giác GMN = tam giác GBC => góc NMG và góc CBG (2 góc tương ứng). Mà góc NMG và góc CBG ở vị trí so le trong nên MN // BC
a) Ta có DM = DG => GM = 2GD. Ta lại có G laf giao điểm của BD và CE => G là trọng tâm của tam giác ABC. => BG = 2GD. => BG = GM. Chứng minh tương tự ta được CG = GN. b)Xét tam giác GMN và tam giác GBC. Có GM = GB (cmt). Góc GMN = góc BGC (2 góc đối đỉnh). GN = GC (cmt). => Tam giác GMN = tam giác GBC ( c.g.c). => MN = BC (2 cạnh tương ứng). Theo chứng minh trên tam giác GMN = tam giác GBC => góc NMG và góc CBG (2 góc tương ứng). Mà góc NMG và góc CBG ở vị trí so le trong nên MN // BC
 a) Xét tam giác ABD có C là trung điểm của cạnh AD => BC là trung tuyến của tam giác ABD. Hơn nữa G thuộc BC và GB = 2GC => GB = 2/3 BC => G là trọng tâm tam giác ABD. Lại có AE là đường trung tuyến của tâm giác ABD nên A, G, E thẳng hàng b) Ta có G là trọng tâm tam giác ABD => DG là đường trung tuyến của tam giác này. Suy ra DG đi qua trung điểm của cạnh AB
a) Xét tam giác ABD có C là trung điểm của cạnh AD => BC là trung tuyến của tam giác ABD. Hơn nữa G thuộc BC và GB = 2GC => GB = 2/3 BC => G là trọng tâm tam giác ABD. Lại có AE là đường trung tuyến của tâm giác ABD nên A, G, E thẳng hàng b) Ta có G là trọng tâm tam giác ABD => DG là đường trung tuyến của tam giác này. Suy ra DG đi qua trung điểm của cạnh AB
 Xét tam giác ABC có hai đường trung tuyến BM và CN cắt tại G. Suy ra G là trọng tâm tam giác ABC. => BG = 2/3 BM; CG = 2/3 CN. => BM = 3/2 BG; CN = 3/2 CG. Do đó 3/2 BG + 3/2 CG > 3/2 BC hay BG + CN > BC (1) Bất đẳng thức (1) luôn đúng vì trong một tâm giác tổng độ dài hai cạnh lớn hơn độ dài cạnh còn lại. Vậy BM + CN > 3/2 BC
Xét tam giác ABC có hai đường trung tuyến BM và CN cắt tại G. Suy ra G là trọng tâm tam giác ABC. => BG = 2/3 BM; CG = 2/3 CN. => BM = 3/2 BG; CN = 3/2 CG. Do đó 3/2 BG + 3/2 CG > 3/2 BC hay BG + CN > BC (1) Bất đẳng thức (1) luôn đúng vì trong một tâm giác tổng độ dài hai cạnh lớn hơn độ dài cạnh còn lại. Vậy BM + CN > 3/2 BC