• 
• Lớp 8
• Toán 8 (Hỗ trợ học bộ Kết nối tri thức với cuộc sống)
• Đề số 1 (có file word + ma trận đặc tả)

• PTPhạm Tiến Dũng

  
  

Phần tự luận (8 điểm)

Bài 1

Bài 1. (1 điểm) Giải các phương trình sau:

a) \(2 x = 7 + x\).

b) \(\frac{x - 3}{5} + \frac{1 + 2 x}{3} = 6\).

Hướng dẫn giải:

a) \(2 x = 7 + x\)

\(2 x - x = 7\)

\(x = 7\).

Phương trình đã cho có nghiệm \(x = 7\).

b) \(\frac{x - 3}{5} + \frac{1 + 2 x}{3} = 6\)

\(\frac{3 \left(\right. x - 3 \left.\right)}{15} + \frac{5. \left(\right. 1 + 2 x \left.\right)}{15} = 6\)

\(3 x - 9 + 5 + 10 x = 90\)

\(13 x = 94\)

\(x = \frac{94}{13}\).

Phương trình đã cho có nghiệm \(x = \frac{94}{13}\).

Bài 2

Bài 2. (2,0 điểm)

1) Cho hai đường thẳng sau: \(\left(\right. d_{1} \left.\right) : \&\text{nbsp}; y = - 3 x\); \(\left(\right. d_{2} \left.\right) : y = x + 2\).

a) Vẽ đường thẳng \(\left(\right. d_{1} \left.\right)\) trên mặt phẳng tọa độ \(O x y\).

b) Tìm \(a , b\) để đường thẳng \(\left(\right. d_{3} \left.\right) : y = a x + b\) đi qua điểm \(A \left(\right. - 1 ; 3 \left.\right)\) và song song với \(\left(\right. d_{2} \left.\right)\).

2) Theo kế hoạch hai tổ sản xuất phải làm \(900\) sản phẩm. Do cải tiến kĩ thuật nên tổ I vượt mức \(20 \%\) và tổ II vượt mức \(15 \%\) so với kế hoạch. Do đó trên thực tế hai tổ đã sản xuất được \(1\) \(055\) sản phẩm. Hỏi theo kế hoạch mỗi tổ sản xuất được bao nhiêu sản phẩm?

Bài 3

Bài 3. (1,0 điểm) Một túi đựng \(19\) viên bi cùng khối lượng và kích thước, chỉ khác màu, trong đó có \(8\) viên bi màu đỏ, \(5\) viên bi màu xanh và \(6\) viên bi màu vàng. Lấy ngẫu nhiên một viên bi từ trong túi. Tính xác suất của biến cố "Lấy được viên bi màu đỏ".

Bài 4

Bài 4. (2,5 điểm) Cho tam giác \(K B C\) vuông tại \(K\) (\(K B < K C\)). Tia phân giác của \(\hat{B}\) cắt cạnh \(K C\) tại \(H\). Qua \(C\) vẽ đường thẳng vuông góc với tia \(B H\) cắt đường thẳng \(B H\) tại \(I\).

a) Chứng minh tam giác \(B H K\) đồng dạng với tam giác \(C H I\).

b) Chứng minh \(C I^{2} = I H . I B\).

c) Tia \(B K\) cắt tia \(C I\) tại \(A\), tia \(A H\) cắt \(B C\) tại \(D\). Chứng minh \(K C\) là tia phân giác của \(\hat{I K D}\).

Bài 5

Bài 5. (1 điểm) Bạn Đô làm một cái lồng đèn quả trám là hình ghép từ hai hình chóp tứ giác đều giống nhau có cạnh đáy \(20\) cm, cạnh bên \(32\) cm. Khoảng cách giữa hai đỉnh của hai hình chóp là \(30\) cm.

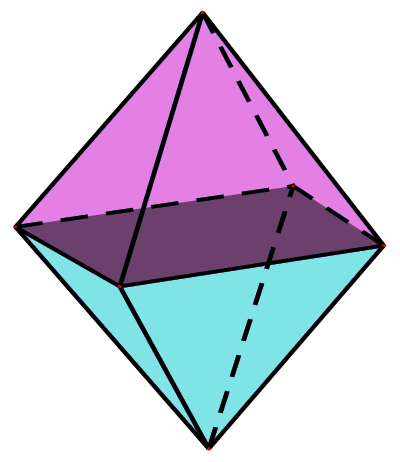
Tính thể tích của lồng đèn.

Bài 6

Bài 6. (0,5 điểm) Tính diện tích tam giác có độ dài ba cạnh bằng \(10\) cm, \(17\) cm, \(21\) cm.