

Phạm Thị Thủy
Giới thiệu về bản thân



































a) 3x(x-1)-1+x=0
⇔3x(x-1)-(x-1)=0
⇔(3x-1)(x-1)=0
TH1: 3x-1=0
⇔ 3x=1
⇔ x=1/3
TH2: x-1=0
⇔ x=1
Vậy x ϵ (1/3; 1)
b) x2 - 9x = 0
⇔x (x-9)=0
TH1: x=0
TH2: x-9=0
⇔ x=9
Vậy x ϵ (0; 9)
a) x2 + 25 - 10x= x2 - 10x + 25= (x-5)2
b) -8y3 + x3= x3 - 8y3= (x-2y).(x2+2xy+4y2)
a) (2x+1)2= 2x2 + 2.2x.1 + 12= 4x2 + 4x + 1
b) (a - b/2)3= a3 - 3.a2.b/2 + 3.a.(b/2)2 - (b/2)3= a3 - 3/2a2b + 3/4ab2 - 1/8b3
a) Xét và có:
chung;
;
Do đó (g.g).
Suy ra nên .
b) Từ suy ra .
Xét và có:
(cmt);
chung;
Do đó (c.g.c)
Suy ra (cặp góc tương ứng).
c) Xét và có:
chung;
Do đó (g.g)
Suy ra (cặp cạnh tương ứng).
Xét và có:
(cmt);
chung;
Do đó (c.g.c)
Suy ra (cặp góc tương ứng) (1)
Tương tự: (2).
Từ (1) và (2) suy ra .
Mà suy ra .
Suy ra là phân giác của góc .
Mặt khác nên là phân giác ngoài của .
Ta có là phân giác trong của suy ra (3)
Ta có là phân giác ngoài của suy ra (4)
Từ (3) và (4) suy ra .
a) Với , hàm số trở thành .
Xét hàm số :
Thay thì .
Suy ra đồ thị hàm số đi qua điểm có tọa độ .
Thay thì .
Suy ra đồ thị hàm số đi qua điểm có tọa độ .
Vẽ đồ thị:
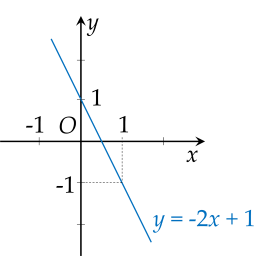
b) Vì đường thẳng song song với đường thẳng nên: .
Khi đó ta có: và .
Vì đường thẳng đi qua nên:
Suy ra (thoả mãn)
Vậy đường thẳng cần tìm là .
Đổi 20p=\(\dfrac{1}{3}\)h
Gọi quãng đường từ thành phố về quê là x(x>0, km)
Thời gian xe máy đi từ thành phố về quê là: \(\dfrac{x}{30}\)km/h
Thời gian xe máy đi từ quê lên thành phố là: \(\dfrac{x}{25}\)km/h
Vì thời gian lúc lên thành phố nhiều hơn thời gian về quê là phút nên ta có phương trình:
\(\dfrac{x}{25}\) - \(\dfrac{x}{30}\) = \(\dfrac{1}{3}\)
<=> \(\dfrac{6x}{150}\) - \(\dfrac{5x}{150}\) = \(\dfrac{50}{150}\) <=> 6x-5x=50 <=> x=50(tm) Vậy quãng đường từ thành phố về quê là 50km