

Vũ Hải Linh
Giới thiệu về bản thân



































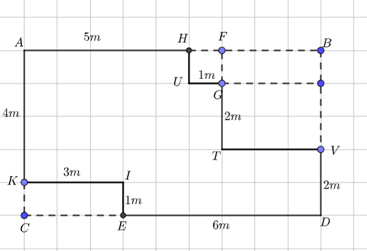
Gọi \(S\) là diện tích mảnh vườn.
\(S_{A B D C} = S_{K I E C} + S_{H F G U} + S_{F B V T} + S\)
Suy ra \(S = S_{A B D C} - S_{K I E C} - S_{H F G U} - S_{F B V T}\)
\(S = 9.5 - 3.1 - 1.1 - 3.3 = 32\) (m\(^{2}\)).
Gọi \(a\) là số học sinh cần tìm, \(a\) là số tự nhiên.
Ta có: \(a 2\); \(a \&\text{nbsp}; \&\text{nbsp}; 3\); \(a \&\text{nbsp}; \&\text{nbsp}; 5\) và \(430 \leq a \leq \&\text{nbsp}; 460\)
Suy ra \(a \in\) BC\(\left(\right. 2 ; 3 ; 5 \left.\right)\) và \(430 \leq \&\text{nbsp}; a \leq \&\text{nbsp}; 460\)
BCNN\(\left(\right. 2 ; 3 ; 5 \left.\right) = 2.3.5 = 30\)
BC\(\left(\right. 2 ; 3 ; 5 \left.\right) =\) B\(\left(\right. 30 \left.\right) = \left{\right. 0 ; 30 ; 60 ; \ldots ; 300 ; 330 ; 360 ; \&\text{nbsp}; 390 ; 420 ; 450 ; 480 ; \ldots \left.\right}\)
Vì \(430 \leq \&\text{nbsp}; a \leq \&\text{nbsp}; 460\) nên \(a = 450\).
Vậy số học sinh cần tìm là \(450\) học sinh.
a) Ba cạnh bằng nhau: AB = BC = CA;
Ba góc ở các đỉnh A, B, C bằng nhau.
Tổng số tiền mua \(2\) cái áo phông, \(3\) cái quần soọc và \(5\) cái khăn mặt là:
\(2.125\) \(000 + 3.95\) \(000 + 5.17\) \(000 = 620\) \(000\) (đồng)
Số tiền anh Đô cần phải trả thêm là:
\(620\) \(000 - \&\text{nbsp}; 2.100\) \(000 = 420\) \(000\) (đồng).
a) 8 = VIII; 15 = XV; 24 = XXIV.
b) Các bội nhỏ hơn 10 của số 3 là: 0; 3; 6 và 9.
k