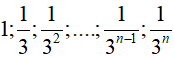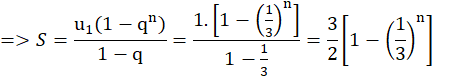a, Phân tử methane (CH4) : Nguyên tử C có 4e ở lớp ngoài cùng , cần 4e để có lớp vỏ bền vững , nguyên tử h có 1e ở lớp ngoài cùng cần 1e nx để có lớp vỏ bền vững ->C sẽ hình thành 4 liên kết cộng hóa trị đơn với 4 nguyên tử H, mỗi liên kết do C và H góp chung 1 electron.

b,Nguyên tử N có 5 electron lớp ngoài  cần thêm 3e để có lớp vỏ bền vững , mỗi nguyên tử H có 1e, cần thêm 1e để có lớp vỏ bền vững ->N sẽ tạo 3 liên kết cộng hóa trị đơn với 3 nguyên tử H, chia sẻ 1 cặp e cho mỗi liên kết.

c,Nguyên tử C có 4e lớp ngoài, cần thêm 4e để có cấu trúc lớp vỏ bền vững , Mỗi nguyên tử O  có 6e lớp ngoài, cần thêm 2e để có lớp vỏ bền vững ->C sẽ tạo 2 liên kết đôi với 2 nguyên tử O (mỗi O chia sẻ 2e với C).

(CHÚC BẠN HỌC TỐT )

Trong gia đình, cha mẹ là người yêu thương ta hơn bao giờ hết. Cha mẹ là người sinh ra, nuôi dưỡng ta khôn lớn trưởng thành. Nhưng khi ta lớn lên cũng là lúc tóc bạc lốm đốm trên tóc, khi nụ cười cha mẹ hằn vết nhăn. Mái ấm tình thương luôn gắn liền với hi sinh, với bao sẻ chia mà cha mẹ cho ta.

Phép nối: nhưng

Tham khảo nha!!!!

Để chứng minh rằng trong tam giác nhọnABC vớiAB<AC, và đường caoAH từA tớiBC, ta có△AMH∼△AHB và từ đó suy ra đượcAH2=AM⋅AB, cũng nhưAN⋅AC=AM⋅AB.

### 1. Chứng minh△AMH∼△AHB

- Từ định nghĩa hình chiếu, ta có∠AMH=90∘ vìHM⊥AB và∠AHB=90∘ bởiAH là đường cao trong tam giácABC.
- Cả hai tam giácAMH vàAHB đều có gócA chung.
- Do đó, theo tiêu chí góc-góc (AA), ta có:

△AMH∼△AHB

### 2. Suy raAH2=AM⋅AB

Từ tính chất của hai tam giác giống nhau (tỷ lệ các cạnh tương ứng), ta có:

AMAB=AHAM⟹AH⋅AB=AM2⟹AH2=AM⋅AB

### 3. Chứng minhAN⋅AC=AM⋅AB

Tạo dựng các tam giác và hình chiếu như sau:

- KhiN là hình chiếu củaH trênAC, ta cũng áp dụng tương tự với△ANH và△AHB.
- Từ tính chất của các tam giác vuông, có:

ANAC=AHAB⟹AN⋅AC=AH⋅AB

ThayAH bằngAM2AB từ kết quả trước:

AN⋅AC=AM⋅AB

### Kết luận

Từ các phương trình và định lý trên, chúng ta đã chứng minh được các kết quả yêu cầu:

1.△AMH∼△AHB,
2.AH2=AM⋅AB,
3.AN⋅AC=AM⋅AB.

Chúc bạn học tốt!!!!

Ta có:  lập thành cấp số nhân có:u1 = 1, q = 1/3