Nửa chu vi tam giác:

\(\frac{\left(\right. 10 + 17 + 21 \left.\right)}{2} = 24 \left(\right. c m \left.\right)\)

Diện tích tam giác:

\(S = \sqrt{24. \left(\right. 24 - 10 \left.\right) . \left(\right. 24 - 17 \left.\right) . \left(\right. 24 - 21 \left.\right)} = 84 \left(\right. c m^{2} \left.\right)\)

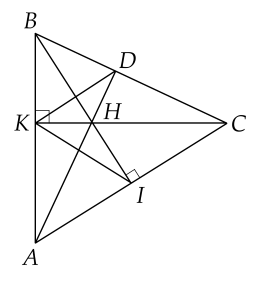
a) Vì tam giác 𝐾𝐵𝐶KBC vuông tại 𝐾K suy ra 𝐾𝐵𝐻^=90∘KBH=90∘

Vì 𝐶𝐼⊥𝐵𝐼CI⊥BI (gt) suy ra 𝐶𝑙𝐻^=90∘ClH=90∘

Xét △𝐾𝐵𝐻△KBH và △𝐶𝐻𝐼△CHI có:

𝐾𝐵𝐻^=𝐶𝐼𝐻^=90∘KBH=CIH=90∘;

𝐵𝐻𝐾^=𝐶𝐻𝐼^BHK=CHI (đối đỉnh)

Suy ra Δ𝐵𝐻𝐾∽Δ𝐶𝐻𝐼ΔBHK∽ΔCHI (g.g)

b) Ta có Δ𝐵𝐻𝐾∽Δ𝐶𝐻𝐼ΔBHK∽ΔCHI suy ra 𝐻𝐵𝐾^=𝐻𝐶𝐼^HBK=HCI (hai góc tương ứng) 

Mà 𝐵𝐻BH là tia phân giác của 𝐴𝐵𝐶^ABC nên 𝐻𝐵𝐾^=𝐻𝐵𝐶^HBK=HBC.

Do đó 𝐻𝐵𝐶^=𝐻𝐶𝐼^HBC=HCI.

Xét △𝐶𝐼𝐵△CIB và △𝐻𝐼𝐶△HIC có:

𝐶𝐼𝐵^CIB chung;

𝐼𝐵𝐶^=𝐻𝐶𝐼^IBC=HCI (cmt)

Vậy Δ𝐶𝐼𝐵≈Δ𝐻𝐼𝐶ΔCIB≈ΔHIC (g.g) suy ra 𝐶𝐼𝐻𝐼=𝐼𝐵𝐼𝐶HICI​=ICIB​

Hay 𝐶𝐼2=𝐻𝐼.𝐼𝐵CI2=HI.IB

c) Xét △𝐴𝐵𝐶△ABC có 𝐵𝐼⊥𝐴𝐶BI⊥AC; 𝐶𝐾⊥𝐴𝐵CK⊥AB; 𝐵𝐼∩𝐶𝐾={𝐻}BI∩CK={H}

Nên 𝐻H là trực tâm △𝐴𝐵𝐶△ABC suy ra 𝐴𝐻⊥𝐵𝐶AH⊥BC tại 𝐷D.

Từ đó ta có △𝐵𝐾𝐶∽△𝐻𝐷𝐶△BKC∽△HDC (g.g) nên 𝐶𝐵𝐶𝐻=𝐶𝐾𝐶𝐷CHCB​=CDCK​

Suy ra 𝐶𝐵𝐶𝐾=𝐶𝐻𝐶𝐷CKCB​=CDCH​ nên △𝐵𝐻𝐶∽△𝐾𝐷𝐶△BHC∽△KDC (c.g.c)

Khi đó 𝐻𝐵𝐶^=𝐷𝐾𝐶^HBC=DKC (hai góc tương ứng)

Chứng minh tương tự 𝐻𝐴𝐶^=𝐼𝐾𝐶^HAC=IKC

Mà 𝐻𝐴𝐶^=𝐻𝐵𝐶^HAC=HBC (cùng phụ 𝐴𝐶𝐵^ACB )

Suy ra  𝐷𝐾𝐶^=𝐼𝐾𝐶^ DKC=IKC.

Vậy 𝐾𝐶KC là tia phân giác của 𝐼𝐾𝐷^IKD.

Số kết quả có thể là: 19

Số kết quả thuận lợi là: 8

Xác suất của biến cố A: " Lấy được viên bi màu đỏ "

\(pa=\frac{8}{19}\)

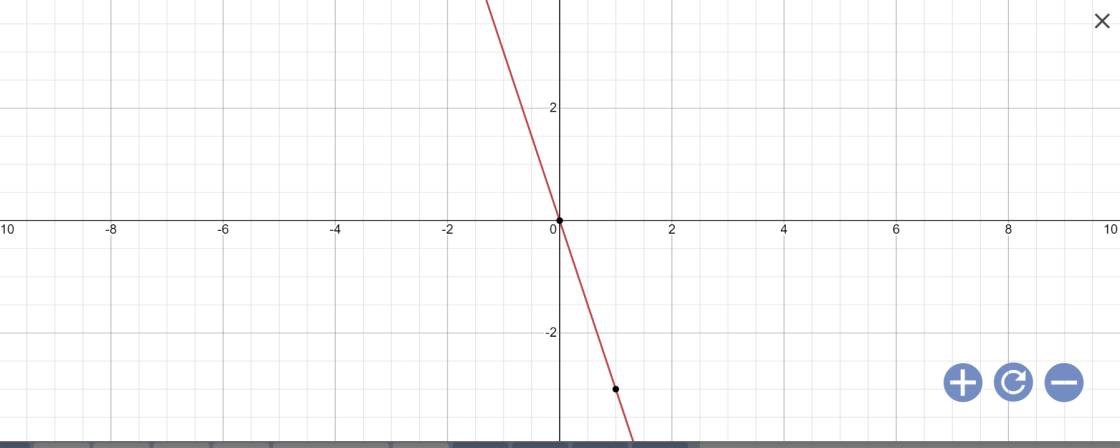
b) Vì (d3)//(d2) nên \(a=1;b\neq2\)

Vậy (d3): y=x+b

Thay x=-1 và y=3 vào (d3), ta được:

b-1=3

=>b=4

Vậy: (d3): y=x+4

Bài 2:

Gọi số sản phẩm tổ 1 phải sản xuất theo kế hoạch là x(sản phẩm)

(ĐIều kiện: \(x \in Z^{+}\))

Số sản phẩm tổ 2 phải sản xuất theo kế hoạch là:

900-x(sản phẩm)

Số sản phẩm thực tế tổ 1 làm được là:

\(x \left(\right. 1 + 20 \% \left.\right) = 1 , 2 x \left(\right. s ả n p h ẩ m \left.\right)\)

Số sản phẩm thực tế tổ 2 làm được là:

\(\left(\right. 900 - x \left.\right) \left(\right. 1 + 15 \% \left.\right) = 1 , 15 \left(\right. 900 - x \left.\right) \left(\right. s ả n p h ẩ m \left.\right)\)

Tổng sản phẩm là 1055 sản phẩm nên :

1,2x+1,15(900-x)=1055

0,05x+1035=1055

0,05x = 20

x = 400(nhận)

Vậy số sản phẩm tổ 1 phải sản xuất theo kế hoạch là 400 sản phẩm

Vậy số sản phẩm tổ 2 phải sản xuất theo kế hoạch là 900-400=500 sản phẩm

a) 2x = 7 + x

2x - x = 7

x = 7

Vậy phương trình có nghiệm x = 7

b) x - 3 / 5 + 1 + 2x / 3 = 6

(x - 3) . 3 / 5 . 3 + (1 + 2x) . 5 / 3 . 5 = 6 . 15 / 15

3x - 9 / 15 + 5 + 10x / 15 = 90

3x - 9 + 5 + 10x = 90

3x + 10x = 90 + 9 - 5

13x = 94

x = 94 / 13

Vậy phương trình có nghiệm x = 94/13

Nội thủy: là vùng nước tiếp giáp với bờ biển, ở phía trong đường cơ sở và là bộ phận lãnh thổ của Việt Nam.

Lãnh hải: có chiều rộng là 12 hải lí tính từ đường cơ sở ra phía biển. Ranh giới ngoài của lãnh hải là biên giới quốc gia trên biển Việt Nam.

Vùng tiếp giáp lãnh hải: là vùng biển tiếp liền và nằm ngoài vùng lãnh hải Việt Nam, có chiều rộng là 12 hải lí tính từ ranh giới ngoài của lãnh hải.

Vùng đặc quyền kinh tế: là vùng biển tiếp liền và nằm ngoài vùng lãnh hải Việt Nam, hợp với lãnh hải tạo thành một vùng biển có chiều rộng 200 hải lí tính từ đường cơ sở.

Thềm lục địa: Là vùng đáy biển và lòng đất dưới đáy biển, tiếp liền và nằm ngoài lãnh hải Việt Nam, trên toàn bộ phần kéo dài tự nhiên của lãnh thổ đất liênd, các đảo và quần đảo của Việt Nam cho đến mép ngoài của rìa lục địa. Ranh giới ngoài thềm lúc địa cách đường cơ sở không quá 350 hải lí.

câu D. chemistry

Renewable sources like wind energy, solar energy, bioenergy, geothermal energy, etc...

theo em, nhà thơ đã thể hiện cảm xúc thích thú và tận hưởng vẻ đẹp của trời mưa mỗi khi nó đến. Ông đã mô tả mọi người với vẻ hạnh phúc và mong chờ mỗi khi đến mùa mưa. Qua những câu thơ trên, nhà thơ cũng thể hiện được tình yêu quê hương sâu đậm, được thể hiện bằng những lời giản dị nhưng giàu cảm xúc. Con người cũng như muốn hòa mình vào thiên nhiên để cảm nhận sự tuyệt vời mỗi khi trời mưa đến.

Em hiểu được rằng mỗi lần ta ra bến chờ thì ta khao khát được hóa thân thành phù sao để tận hưởng không khí và vẻ đẹp mỗi khi mùa mưa đến. Làm tăng sự thân thiết giữa thiên nhiên và con người. Ta có thể chảy theo dòng mưa để đi chu du mọi nơi.