

Nguyễn Anh Hiệp
Giới thiệu về bản thân



































giải:
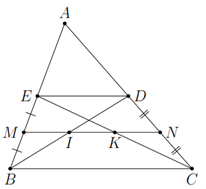
Xét ΔBEDΔBED có {MI//EDME=BM{MI//EDME=BM suy ra ID=IBID=IB.
Xét ΔCEDΔCED có {NK//EDNC=ND{NK//EDNC=ND suy ra KE=KCKE=KC.
Suy ra MI=12EDMI=21ED; NK=12EDNK=21ED; ED=12BCED=21BC.
IK=MK−MI=12BC−12DE=DE−12DE=12DEIK=MK−MI=21BC−21DE=DE−21DE=21DE.
Vậy MI=IK=KNMI=IK=KN.
giải:
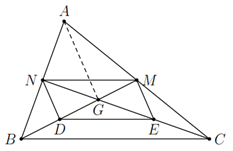
a) Vì BMBM, CNCN là các đường trung tuyến của ΔABCΔABC nên MA=MCMA=MC, NA=NBNA=NB.
Do đó MNMN là đường trung bình của Δ ABCΔ ABC, suy ra MNMN // BCBC. (1)
Ta có DEDE là đường trung bình của Δ GBCΔ GBC nên DEDE // BCBC. (2)
Từ (1) và (2) suy ra MNMN // DEDE.
b) Xét Δ ABGΔ ABG, ta có NDND là đường trung bình.
Xét Δ ACGΔ ACG, ta có MEME là đường trung bình.
Do đó NDND // AGAG, MEME // AGAG.
Suy ra NDND // MEME.
giải:
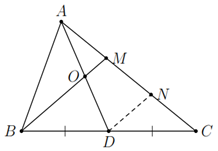
a) Qua DD vẽ một đường thẳng song song với BMBM cắt ACAC tại NN.
Xét Δ MBCΔ MBC có DB=DCDB=DC và DNDN // BMBM nên MN=NC=12MCMN=NC=21MC (định lí đường trung bình của tam giác).
Mặt khác AM=12MCAM=21MC, do đó AM=MN=12MCAM=MN=21MC.
Xét Δ ANDΔ AND có AM=MNAM=MN và BMBM // DNDN nên OA=ODOA=OD hay OO là trung điểm của ADAD.
b) Xét Δ ANDΔ AND có OMOM là đường trung bình nên OM=12DNOM=21DN. (1)
Xét Δ MBCΔ MBC có DNDN là đường trung bình nên DN=12BMDN=21BM. (2)
Từ (1) và (2) suy ra OM=14BMOM=41BM.
giải:
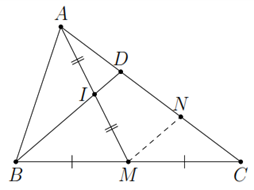
a) Kẻ MNMN // BDBD, N∈ACN∈AC.
MNMN là đường trung bình trong △CBD△CBD
Suy ra NN là trung điểm của CDCD (1).
ININ là đường trung bình trong △AMN△AMN
Suy ra DD là trung điểm của ANAN (2).
Từ (1) và (2) suy ra AD=12DCAD=21DC.
b) Có ID=12MNID=21MN; MN=12BDMN=21BD, nên BD=IDBD=ID.
Xét tam giác ABCABC có BC⊥ AB′BC⊥ AB′ và B′C′⊥AB′B′C′⊥AB′ nên suy ra BCBC // B′C′B′C′.
Theo hệ quả định lí Thalès, ta có: ABAB′ =BCBC′AB′AB =BC′BC
Suy ra xx+h =aa′x+hx =a′a
a′.x=a(x+h)a′.x=a(x+h)
a′.x−ax=aha′.x−ax=ah
x(a′−a)=ahx(a′−a)=ah
x=aha′ −ax=a′ −aah.
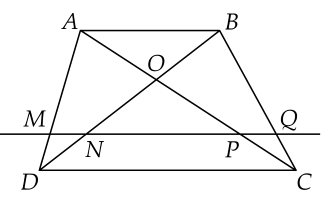
Trong tam giác ADBADB, ta có: MNMN // ABAB (gt)
Suy ra DNDB =MNABDBDN =ABMN (hệ quả định lí Thalès) (1)
Trong tam giác ACBACB, ta có: PQPQ // ABAB (gt)
Suy ra CQCB =PQABCBCQ =ABPQ (hệ quả định lí Thalès) (2)
Lại có: NQNQ // ABAB (gt); ABAB // CDCD (gt)
Suy ra NQNQ // CDCD
Trong tam giác BDCBDC, ta có: NQNQ // CDCD (chứng minh trên)
Suy ra DNDB =CQCBDBDN =CBCQ (định lí Thalès) (3)
Từ (1), (2) và (3) suy ra MNAB =PQAB hayABMN =ABPQ hayMN = PQ$ (đpcm).
Khi đó, ADAD là đường trung tuyến của tam giác ABCABC.
Vì GG là trọng tâm của tam giác ABCABC nên điểm GG nằm trên cạnh ADAD.
Ta có AGAD=23ADAG=32 hay AG=23ADAG=32AD.
Vì MGMG // ABAB, theo định lí Thalès, ta suy ra: AGAD=BMBD=23ADAG=BDBM=32.
Ta có BD=CDBD=CD (vì DD là trung điểm của cạnh BCBC) nên BMBC=BM2BD=22.3=13BCBM=2BDBM=2.32=31.
Do đó BM=13BCBM=31BC (đpcm).
ABCD là hình thang suy ra ABAB // CDCD.
Áp dụng hệ quả định lí Thalès, ta có: OAOC =OBODOCOA =ODOB
Suy ra OA.OD=OB.OCOA.OD=OB.OC (đpcm).
Áp dụng định lí Thalès trong tam giác:
DEDE // ACAC nên AEAB=CDBCABAE=BCCD;
DFDF // ACAC nên AFAC=BDBCACAF=BCBD.
Khi đó, AEAB+AFAC=CDBC+BDBC=BCBC=1ABAE+ACAF=BCCD+BCBD=BCBC=1.