B

nAgNO3​​=1.0,5=0,5(mol);nHCl​=2.0,3=0,6(mol)

PTHH: AgNO₃ + HCl → AgCl ↓ + HNO₃

Mol:      0,5          0,5                          0,5

Ta có: \(\frac{0 , 5}{1} < \frac{0 , 6}{1}\)⇒ AgNO₃ pứ hết, HCl dư

* V_{dd sau pứ} = 0,5+0,6 = 1,1 (l)

\(\Rightarrow C_{M_{d d N O_{3}}} = \frac{0 , 5}{1 , 1} = 0 , 4545 M\)

\(C_{M_{d d H C l d ư}} = \frac{0 , 6 - 0 , 5}{1 , 1} = 0 , 0909 M\)

\(m_{d d A g N O_{3}} = 500.1 , 2 = 600 \left(\right. g \left.\right) ; m_{d d H C l} = 300.1 , 5 = 450 \left(\right. g \left.\right)\)

* m_{dd sau pứ} = 600+450 = 1050 (g)

\(C \%_{d d H N O_{3}} = \frac{0 , 5.63.100 \%}{1050} = 3 \%\)

\(C \%_{d d H C l} = \frac{\left(\right. 0 , 6 - 0 , 5 \left.\right) . 36 , 5.100 \%}{1050} = 0 , 348 \%\)

Diện tích hình chữ nhật là:

22 x 12 = 264 (cm²)

Chiều cao của hình tam giác là:

30 - 22 = 8 (cm)

Độ dài đáy của hình tam giác là:

6 + 12 + 6 = 24 (cm)

Diện tích hình tam giác là:

\(\frac{24 \times 8}{2} = 96 \left(\right. c m^{2} \left.\right)\)

Diện tích tấm bảng chỉ dẫn là:

96 + 264 = 360 (cm²)

đáp số: 360 (cm²)

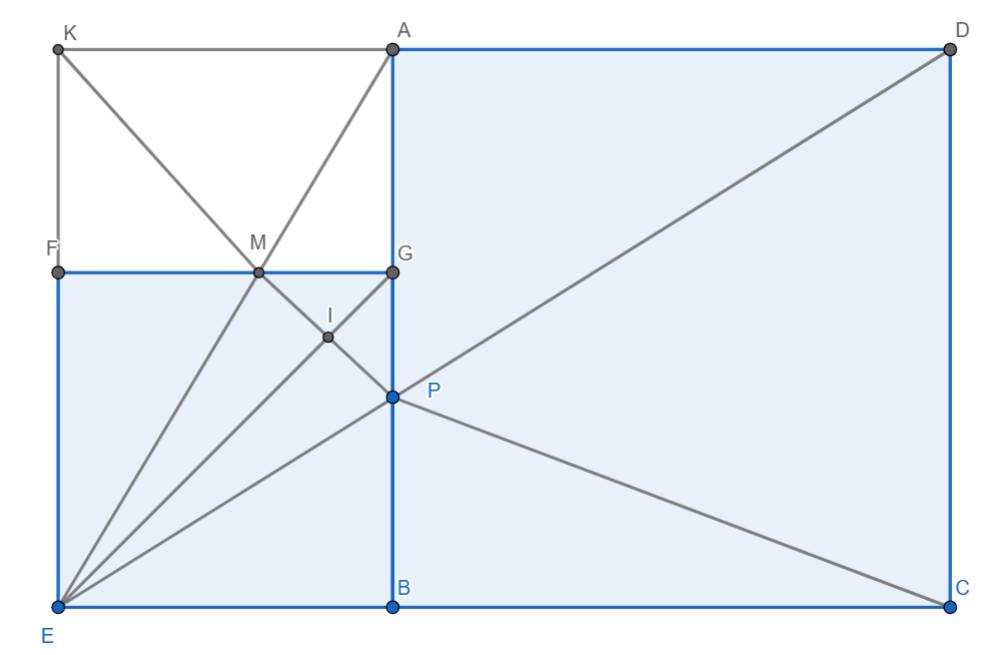
a) \(S_{E A G} = \frac{1}{2} \times A G \times E D = \frac{1}{2} \times 2 \times 3 = 3 \left(\right. c m^{2} \left.\right)\)

\(S_{P B C} = \frac{1}{2} \times B C \times D C = \frac{1}{2} \times 5 \times 5 = 12 , 5 \left(\right. c m^{2} \left.\right)\)

b) Ta có:

\(S_{E B C} = \frac{1}{2} \times B C \times E C = \frac{1}{2} \times 5 \times 8 = 20 \left(\right. c m^{2} \left.\right)\)

\(S_{P E C} = S_{E C B} - S_{P B C} = 20 - 12 , 5 = 7 , 5 \left(\right. c m^{2} \left.\right)\)

Vậy nên:

\(P D = \frac{2 \times S_{P E C}}{E C} = \frac{2 \times 7 , 5}{8} = 1 , 875 \left(\right. c m \left.\right)\)

c) Ta thấy:

\(\frac{I M}{I P} = \frac{S_{M I G}}{S_{I P G}} = \frac{S_{M I E}}{S_{I P E}}\) nên \(\frac{I M}{I P} = \frac{S_{M G E}}{S_{G P E}} = \frac{\frac{1}{2} \times M G \times 3}{\frac{1}{2} \times G P \times 3} = \frac{M G}{G P}\)

Kéo dài AD cắt EF tại K.

Ta có \(S_{A K M} = \frac{1}{2} \times 3 \times 2 = 3 \left(\right. c m^{2} \left.\right)\)

nên \(S_{E K M} = S_{A K E} - S_{A K M} = \frac{1}{2} \times 3 \times 5 - 3 = 4 , 5 \left(\right. c m^{2} \left.\right)\)

Vậy \(F M = \frac{2 \times S_{E K M}}{K E} = 1 , 8 \left(\right. c m \left.\right)\)

Thế thì \(M G = 3 - 1 , 8 = 1 , 2 \left(\right. c m \left.\right)\)

Lại có \(G P = 3 - 1 , 875 = 1 , 125 \left(\right. c m \left.\right)\)

Vậy nên:

\(\frac{I M}{I P} = \frac{M G}{G P} = \frac{1 , 2}{1 , 125} = \frac{16}{15}\).

a)     (-\infty ; \, 2) \cap (-1; \, +\infty)(−∞;2)∩(−1;+∞)=(-1;2)

b)     (−1;6) ∪ [4;8)=(-1;8]

c)      (−∞;−5] ∩(−5;1)={-5}

Tọa độ dỉnh của (P) là: \(I \left(\right. - \frac{b}{2 a} ; \frac{- \Delta}{4 a} \left.\right) \Rightarrow I \left(\right. 1 ; - 4 m - 2 \left.\right)\)

Để I thuộc \(y = 3 x - 1\)

\(\Rightarrow - 4 m - 2 = 3.1 - 1\)

\(\Rightarrow m = - 1\)

6.a.

Với \(a \neq 0\)

 \(\left{\right. 64 a + 8 b + c = 0 \\ - \frac{b}{2 a} = 5 \\ \frac{4 a c - b^{2}}{4 a} = 12\)  \(\Leftrightarrow \left{\right. 64 a + 8 b + c = 0 \\ b = - 10 a \\ 4 a c - b^{2} = 48 a\)

\(\Leftrightarrow \left{\right. c = - 64 a - 8 b = - 64 a - 8 \left(\right. - 10 a \left.\right) = 16 a \\ b = - 10 a \\ 4 a c - b^{2} = 48 a\)

\(\Rightarrow 4 a . 16 a - \left(\left(\right. - 10 a \left.\right)\right)^{2} = 48 a\)

\(\Rightarrow a = - \frac{4}{3} \Rightarrow b = \frac{40}{3} \Rightarrow c = - \frac{64}{3}\)

Hay pt (P): \(y = - \frac{4}{3} x^{2} + \frac{40}{3} x - \frac{64}{3}\)

Vectơ vận tốc trung bình có phương và chiều trùng với vectơ độ dời

Độ lớn của vận tốc trung bình được tính như sau:

\(\mid \overset{\rightarrow}{v_{t b}} \mid = \frac{\mid \overset{\rightarrow}{\Delta r} \mid}{\Delta t} = \frac{12}{1} = 12\) (m/s)

(Do tam giác tạo bởi các vectơ \(\overset{\rightarrow}{r_{1}} , \overset{\rightarrow}{r_{2}} , \overset{\rightarrow}{\Delta r}\) đều)

Số phần tử của dãy số là:

(302-2):3+1=101

Đáp số: 101 số phần tử

a) A={4,5,6,8}

b) B= {x là số tự nhiên khác 7; x≠7;3<x<9}

A={ x là các số tự nhiên chẵn bé hơn 20; x < 20 }