Thực hiện phép nhân, rút gọn rồi tính giá trị biểu thức \(A = x \left(\right. x^{2} - y \left.\right) - x^{2} \left(\right. x + y \left.\right) + y \left(\right. x^{2} + x \left.\right)\) tại \(x = - 95 ,\) \(y = - 814\).

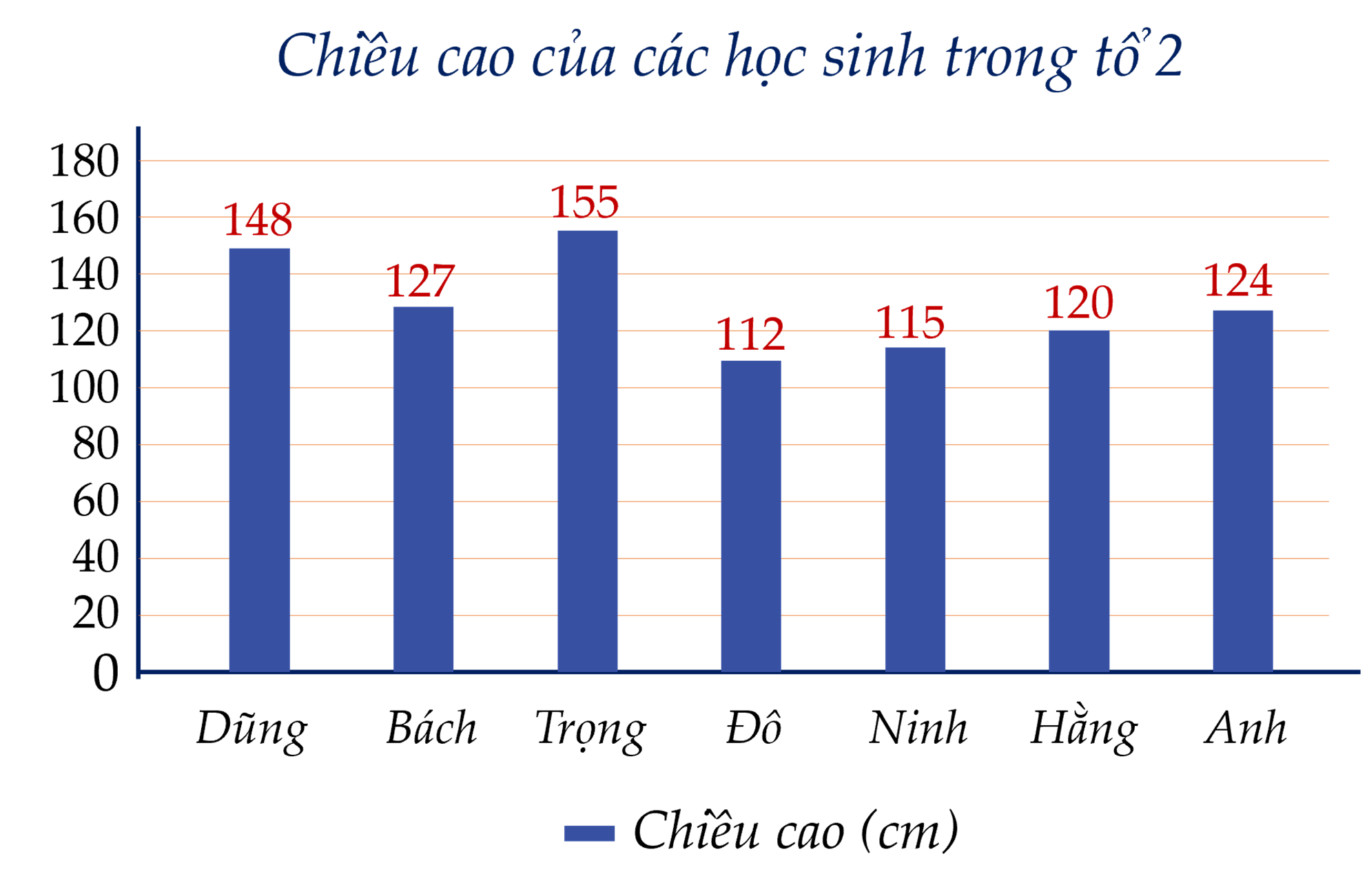
Ta lựa chọn biểu đồ cột.

Vẽ biểu đồ:

x3+y3=(x+y)(x2−xy+y2)=(x+y)(x2+2xy+y2−3xy)

\(= \left(\right. x + y \left.\right) \left[\right. \left(\right. x^{2} + 2 x y + y^{2} \left.\right) - 3 x y \left]\right. = \left(\right. x + y \left.\right) \left[\right. \left(\left(\right. x + y \left.\right)\right)^{2} - 3 x y \left]\right.\).

Với \(x + y = 4\) và \(x y = 3\) ta có \(x^{3} + y^{3} = 4 \left(\right. 4^{2} - 3.3 \left.\right) = 28\).

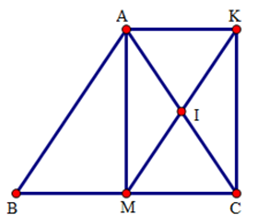
\(\Delta A B C\) cân tại \(A\) có \(A M\) là đường trung tuyến nên \(A M\) là đường cao

Suy ra \(\hat{A M C} = 9 0^{\circ}\).

Xét tứ giác \(A M C K\) có:

   \(I\) là trung điểm \(A C\) (gt)

   \(I\) là trung điểm \(M K\) (\(K\) là điểm đối xứng với \(M\) qua \(I\)).

Do đó \(A M C K\) là hình bình hành.

Lại có \(\hat{A M C} = 9 0^{\circ}\) suy ra \(A M C K\) là hình chữ nhật.

Ta có: \(A K\) // \(M C\) (\(A K C M\) là hình chữ nhật), \(B \in M C\).

Suy ra \(A K\) // \(B M\) (1)

Mà \(A K = M C\) (\(A K C M\)là hình chữ nhật), \(B M = M C\) (\(M\) là trung điểm của \(A C\)).

Suy ra \(A K = B M\) (2)

Từ (1) và (2) ta có \(A K M B\) là hình bình hành.

a) \(x^{2} + 25 - 10 x = x^{2} - 2.5. x + 5^{2} = \left(\left(\right. x - 5 \left.\right)\right)^{2}\)

b) \(- 8 y^{3} + x^{3} = x^{3} - \left(\left(\right. 2 y \left.\right)\right)^{3} = \left(\right. x - 2 y \left.\right) \left(\right. x^{2} + 2 x y + 4 y^{2} \left.\right)\).

a) ĐK: \(x^{2} + 3 x - 4 \neq 0\); \(x + 4 \neq 0\) và \(1 - x \neq 0\) hay \(x \neq 1\); \(x \neq - 4\).

\(P = \frac{10 x}{x^{2} + 3 x - 4} - \frac{2 x - 3}{x + 4} + \frac{x + 1}{1 - x}\)

\(= \frac{10 x}{\left(\right. x - 1 \left.\right) \left(\right. x + 4 \left.\right)} - \frac{2 x - 3}{x + 4} - \frac{x + 1}{x - 1}\)

\(= \frac{10 x - \left(\right. 2 x - 3 \left.\right) \left(\right. x - 1 \left.\right) - \left(\right. x + 1 \left.\right) \left(\right. x + 4 \left.\right)}{\left(\right. x - 1 \left.\right) \left(\right. x + 4 \left.\right)}\)

\(= \frac{10 x - 2 x^{2} + 2 x + 3 x - 3 - x^{2} - 4 x - x - 4}{\left(\right. x - 1 \left.\right) \left(\right. x + 4 \left.\right)}\)

\(= \frac{- 3 x^{2} + 10 x - 7}{\left(\right. x - 1 \left.\right) \left(\right. x + 4 \left.\right)}\)

\(= \frac{- \left(\right. x - 1 \left.\right) \left(\right. 3 x - 7 \left.\right)}{\left(\right. x - 1 \left.\right) \left(\right. x + 4 \left.\right)}\)

\(= \frac{- 3 x + 7}{x + 4}\).

Vậy \(P = \frac{- 3 x + 7}{x + 4}\) với \(x \neq 1 ; x \neq - 4\).

b) Ta có: \(P = \frac{- 3 x + 7}{x + 4}\) với \(x \neq 1 ; x \neq - 4\).

Khi \(x = - 1\) (thỏa mãn điều kiện) thì \(P = \frac{- 3. \left(\right. - 1 \left.\right) + 7}{- 1 + 4} = \frac{10}{3}\).

Vậy khi \(x = - 1\) thì \(P = \frac{10}{3}\).

a) \(A B C D\) là hình bình hành nên hai đường chéo \(A C , B D\) cắt nhau tại \(O\) là trung điểm của mỗi đường.

Xét \(\Delta O B M\) và \(\Delta O D P\) có:

     \(O B = O D\) ( giả thiết)

     \(\hat{O B M} = \hat{O D P}\) (so le trong)

     \(\hat{B O M} = \hat{D O P}\) (đối đỉnh)

Vậy \(\Delta O B M = \Delta O D P\) (g.c.g)

Suy ra \(O M = O P\) (hai cạnh tương ứng)

Chứng minh tương tự \(\Delta O A Q = \Delta O C N\) (g.c.g) suy ra \(O Q = O N\) (hai cạnh tương ứng)

\(M N P Q\) có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.

b) Hình bình hành \(M N P Q\) có hai đường chéo \(M P ⊥ N Q\) nên là hình thoi.

a) \(A B C D\) là hình bình hành nên \(A B = D C\) suy ra \(\frac{1}{2} A B = \frac{1}{2} D C\)

Do đó \(A M = B M = D N = C N\).

Tứ giác \(A M C N\) có \(A M\) // \(N C , A M = N C\) nên là hình bình hành.

Lại có \(\Delta A D C\) vuông tại \(A\) có \(A N\) là đường trung tuyến nên \(A N = \frac{1}{2} D C = D N = C N\).

Hình bình hành \(A M C N\) có hai cạnh kề bằng nhau nên là hình thoi, khi đó hai đường chéo \(A C , M N\) vuông góc với nhau.

Tứ giác \(A M C N\) là hình thoi.

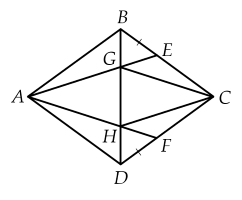
Ta có \(A B C D\) là hình thoi nên \(A C ⊥ B D\) tại trung điểm của mỗi đường nên \(B D\) là trung trực của \(A C\)

Suy ra \(G A = G C , H A = H C\) \(\left(\right. 1 \left.\right)\)

Và \(A C\) là trung trực của \(B D\) suy ra \(A G = A H , C G = C H\) \(\left(\right. 2 \left.\right)\)

Từ \(\left(\right. 1 \left.\right) , \left(\right. 2 \left.\right)\) suy ra \(A G = G C = C H = H A\) nên \(A G C H\) là hình thoi.

1. 

2. Khi rót nước sôi vào phích mà đậy nút ngay lại thì lượng không khí trong phích ở phía trên của nước do nhận được năng lượng nhiệt truyền từ nước, sẽ nóng lên, nhưng bị nút bịt kín nên không nở ra được, gây ra áp suất lớn và đẩy nút bung ra khỏi miệng phích.

Để tránh hiện tượng đó, sau khi rót nước sôi vào phích, cần chờ cho lượng khí này nở ra hết, một phần bay ra khỏi miệng phích, rồi mới đậy nút phích lại.