viets 3 góc 3 cạnh của mỗi hình tam giác dưới đây
các bạn xem sách giáo khoa trang 86 bài 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
B1
21 tháng 8 2017
bài 2
Thử dùng phương pháp đại số để tìm kết quả, thấy như sau:
Gọi a là dài; b là rộng
a + b = (a –b) x 5 ......... a + b = 5a – 5b ........4a = 6b ....... a = 6/4b
a x b = 846
Thay (a) vào: 6/4b x b = 846
bxb = 846 x 4/6 = 564
b = 23,74 (non)
a = 35,76
Thử lại
a x b = 23,74 x 35,76 = 848,9424
a-b= 35,76 – 23,74 = 12,02
a+b= 59,5
(a+b) : (a-b) = 4,95
Số liệu của đề bài hơi khó !!!
21 tháng 8 2017
1,
2/5 số truyện bằng 2/6 số sách giáo khoa . Vậy nếu số truyện là 5 phần thì số sách giáo khoa là 6 phần .
Số quyển truyện : 2310 : ( 5 + 6 ) x 5 = 1050 quyển
Số sách giáo khoa : 2310 - 1050 = 1260 quyển
Đ/S : .........
Sorry vì 2 bài kia ko làm được . tk nha
20 tháng 3 2016
Nếu : ∆ABC cân tại A, M là điểm thuộc cạnh đáy BC, ta chứng minh AM ≤ AB;
AM ≤ AC
+ Nếu M ≡ A hoặc M ≡ B ( Kí hiệu đọc là trùng với) thì AM = AB, AM = AC.
+ Nếu M nằm giữa B và C; ( M ≢ B , C). Gọi H là trung điểm của BC, mà ∆ABC cân tại A nên AH ⊥ BC
+ Nếu M ≡ H => AM ⊥ BC => AM < AB và AM < AC
+ Nếu M ≢ K giả sử M nằm giữa H và C=> MH < CH
Vì MN và CH là hình chiếu MA và CA trên đường BC nên MA < CA => MA < BA
Chứng minh tương tự nếu M nằm giữa H và B thì MA < AB, MA < AC
Vậy mọi giá trị của M trên cạnh đáy BC thì AM ≤ AB, AM ≤ AC
5 tháng 8 2017
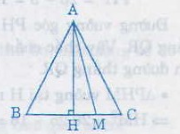
Giả sử ∆ABC cân tại A, M là điểm thuộc cạnh đáy BC, ta chứng minh AM ≤ AB;
AM ≤ AC
+ Nếu M ≡ A hoặc M ≡ B ( Kí hiệu đọc là trùng với) thì AM = AB, AM = AC.
+ Nếu M nằm giữa B và C; ( M ≢ B , C). Gọi H là trung điểm của BC, mà ∆ABC cân tại A nên AH ⊥ BC
+ Nếu M ≡ H => AM ⊥ BC => AM < AB và AM < AC
+ Nếu M ≢ K giả sử M nằm giữa H và C=> MH < CH
Vì MN và CH là hình chiếu MA và CA trên đường BC nên MA < CA => MA < BA
Chứng minh tương tự nếu M nằm giữa H và B thì MA < AB, MA < AC
Vậy mọi giá trị của M trên cạnh đáy BC thì AM ≤ AB, AM ≤ AC
CM
30 tháng 7 2019
Sách giáo khoa Toán 3 nhiều hơn sách giáo khoa Tiếng Việt 3 tập một số trang là :
184 – 160 = 24 (trang)
Đáp số : 24 trang.