giup toi voi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
8 tháng 4 2023
A = \(\dfrac{2x-1}{x+2}\)
a, A là phân số ⇔ \(x\) + 2 # 0 ⇒ \(x\) # -2
b, Để A là một số nguyên thì 2\(x-1\) ⋮ \(x\) + 2
⇒ 2\(x\) + 4 - 5 ⋮ \(x\) + 2
⇒ 2(\(x\) + 2) - 5 ⋮ \(x\) + 2
⇒ 5 ⋮ \(x\) + 2
⇒ \(x\) + 2 \(\in\) { -5; -1; 1; 5}
⇒ \(x\) \(\in\) { -7; -3; -1; 3}
c, A = \(\dfrac{2x-1}{x+2}\)
A = 2 - \(\dfrac{5}{x+2}\)
Với \(x\) \(\in\) Z và \(x\) < -3 ta có
\(x\) + 2 < - 3 + 2 = -1
⇒ \(\dfrac{5}{x+2}\) > \(\dfrac{5}{-1}\) = -5 ⇒ - \(\dfrac{5}{x+2}\)< 5
⇒ 2 - \(\dfrac{5}{x+2}\) < 2 + 5 = 7 ⇒ A < 7 (1)
Với \(x\) > -3; \(x\) # - 2; \(x\in\) Z ⇒ \(x\) ≥ -1 ⇒ \(x\) + 2 ≥ -1 + 2 = 1
\(\dfrac{5}{x+2}\) > 0 ⇒ - \(\dfrac{5}{x+2}\) < 0 ⇒ 2 - \(\dfrac{5}{x+2}\) < 2 (2)
Với \(x=-3\) ⇒ A = 2 - \(\dfrac{5}{-3+2}\) = 7 (3)
Kết hợp (1); (2) và(3) ta có A(max) = 7 ⇔ \(x\) = -3
LD
1
2 tháng 4 2021
Có: 20>0 và x^2 lớn hơn hoặc bằng 0
=>20-x^2 lớn hơn hoặc bằng 0.
Để 20-x^2 có giá trị lớn nhất.
=>20-x^2 bé hơn hoặc bằng 20.
Dấu "=" xảy ra khi: x^2=0=>x=0
Vật: Giá trị lớn nhất của A là 20 khi x=0
DB
Giá trị lớn nhất của biểu thức frac{\sqrt{x}}{x+1} là
(Nhập kết quả dưới dạng số thập phân gọn nhất)
0
CM
14 tháng 6 2018
P có giá trị số lớn nhất khi (x - 6 ) có giá trị bé nhất.
Giá trị bé nhất của (x - 6 ) là: x - 6 = 1
x = 1 + 6
x = 7
Khi đó giá trị số của biểu thức P là:
P = 2004 + 540 : ( 7 - 6 )
= 2004 + 540
= 2544
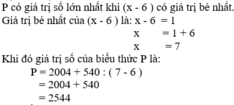
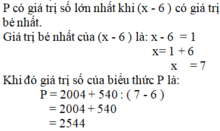
a: \(2x^2+2x+3\)
\(=2\left(x^2+x+\frac32\right)\)
\(=2\left(x^2+x+\frac14+\frac54\right)\)
\(=2\left(x+\frac12\right)^2+\frac52\ge\frac52\forall x\)
=>\(\frac{3}{2x^2+2x+3}\le3:\frac52=\frac65\forall x\)
Dấu '=' xảy ra khi \(x+\frac12=0\)
=>\(x=-\frac12\)
b: \(-x^2+2x-2\)
\(=-\left(x^2-2x+2\right)\)
\(=-\left(x^2-2x+1+1\right)\)
\(=-\left(x-1\right)^2-1\le-1\forall x\)
=>\(\frac{1}{-x^2+2x-2}\ge\frac{1}{-1}=-1\forall x\)
Dấu '=' xảy ra khi x-1=0
=>x=1
c: \(3x^2+4x+15\)
\(=3\left(x^2+\frac43x+5\right)\)
\(=3\left(x^2+2\cdot x\cdot\frac23+\frac49+\frac{41}{9}\right)\)
\(=3\left(x+\frac23\right)^2+\frac{41}{3}\ge\frac{41}{3}\forall x\)
=>\(\frac{5}{3x^2+4x+15}\le5:\frac{41}{3}=\frac{15}{41}\)
=>\(-\frac{5}{3x^2+4x+15}\ge-\frac{15}{41}\forall x\)
Dấu '=' xảy ra khi \(x+\frac23=0\)
=>\(x=-\frac23\)
d: \(-4x^2+8x-5\)
\(=-4\left(x^2-2x+\frac54\right)\)
\(=-4\left(x^2-2x+1+\frac14\right)\)
\(=-4\left(x-1\right)^2-1<=-1\forall x\)
=>\(\frac{2}{-4x^2+8x-5}\ge\frac{2}{-1}=-2\forall x\)
Dấu '=' xảy ra khi x-1=0
=>x=1