Question

[Ngyueenx]

Giải giúp mik vx mik cần gấp ạ

Answer 1

[Nguyễn Lê Phước Thịnh]

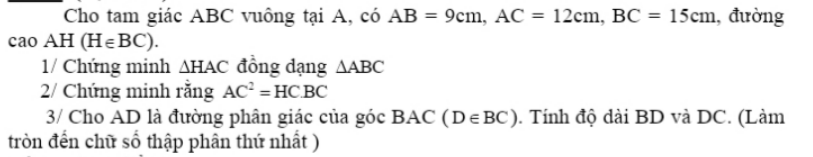
bài 3:

a: \(C=5+5^2+5^3+\cdots+5^{20}\)

\(=5\left(1+5+5^2+\cdots+5^{19}\right)\) ⋮5

b: \(C=5+5^2+5^3+\cdots+5^{20}\)

\(=\left(5+5^2\right)+\left(5^3+5^4\right)+\cdots+\left(5^{19}+5^{20}\right)\)

\(=5\left(1+5\right)+5^3\left(1+5\right)+\cdots+5^{19}\left(1+5\right)\)

\(=6\left(5+5^3+\cdots+5^{19}\right)\) ⋮6

c: \(C=5+5^2+5^3+\cdots+5^{20}\)

\(=\left(5+5^2+5^3+5^4\right)+\left(5^5+5^6+5^7+5^8\right)+\cdots+\left(5^{17}+5^{18}+5^{19}+5^{20}\right)\)

\(=5\left(1+5+5^2+5^3\right)+5^5\left(1+5+5^2+5^3\right)+\cdots+5^{17}\left(1+5+5^2+5^3\right)\)

\(=\left(1+5+5^2+5^3\right)\left(5+5^5+\cdots+5^{17}\right)=156\cdot\left(5+5^5+\cdots+5^{17}\right)\)

\(=13\cdot12\cdot\left(5+5^5+\cdots+5^{17}\right)\) ⋮13

Bài 2:

a: \(B=3+3^2+3^3+\cdots+3^{120}\)

\(=3\left(1+3+3^2+3^3+\cdots+3^{119}\right)\) ⋮3

b: \(B=3+3^2+3^3+\cdots+3^{120}\)

\(=\left(3+3^2\right)+\left(3^3+3^4\right)+\cdots+\left(3^{119}+3^{120}\right)\)

\(=3\left(1+3\right)+3^3\left(1+3\right)+\cdots+3^{119}\left(1+3\right)\)

\(=4\left(3+3^3+\cdots+3^{119}\right)\) ⋮4

c: \(B=3+3^2+3^3+\cdots+3^{120}\)

\(=\left(3+3^2+3^3\right)+\left(3^4+3^5+3^6\right)+\cdots+\left(3^{118}+3^{119}+3^{120}\right)\)

\(=3\left(1+3+3^2\right)+3^4\left(1+3+3^2\right)+\cdots+3^{118}\left(1+3+3^2\right)\)

\(=13\left(3+3^4+\cdots+3^{118}\right)\) ⋮13

Bài 1:

a: \(A=2+2^2+2^3+\ldots+2^{20}\)

\(=2\left(1+2+2^2+\cdots+2^{19}\right)\) ⋮2

b: \(A=2+2^2+2^3+\ldots+2^{20}\)

\(=\left(2+2^2\right)+\left(2^3+2^4\right)+\cdots+\left(2^{19}+2^{20}\right)\)

\(=2\left(1+2\right)+2^3\left(1+2\right)+\cdots+2^{19}\left(1+2\right)\)

\(=3\left(2+2^3+\cdots+2^{19}\right)\) ⋮3

c: \(A=2+2^2+2^3+\ldots+2^{20}\)

\(=\left(2+2^2+2^3+2^4\right)+\left(2^5+2^6+2^7+2^8\right)+\cdots+\left(2^{17}+2^{18}+2^{19}+2^{20}\right)\)

\(=2\left(1+2+2^2+2^3\right)+2^5\left(1+2+2^2+2^3\right)+\cdots+2^{17}\left(1+2+2^2+2^3\right)\)

\(=15\left(2+2^5+\ldots+2^{17}\right)=5\cdot3\cdot\left(2+2^5+\cdots+2^{17}\right)\) ⋮5

Answer 2

[Nguyễn Thị Thương Hoài]

Bài 1:

a; A = 2 + \(2^2\) + 2\(^3\) + ... + 2\(^{20}\)

A = 2 x (1+ 2+ 2\(^2\) + ... + 2\(^{19}\))

A ⋮ 2(đpcm)

b; A = 2 + \(2^2\) + 2\(^3\) + ... + 2\(^{20}\)

Xét dãy số: 1; 2;...; 20 đây là dãy số cách đều với khoảng cách là:

2 - 1 = 1

Số số hạng của dãy số trên là:

(20 - 1) : 1+ 1 = 20(số)

Vì 20 : 2 = 10

Vậy nhóm hai số hạng liên tiếp của A vào nhau khi đó ta có:

A = (2+ 2\(^2\)) + (2\(^3\) + 2\(^4\)) + ... + (2\(^{19}+\) 2\(^{20}\))

A = 2.(1 + 2) + 2\(^3\).(1+ 2) + ... + 2\(^{19}\) .(1 + 2)

A = 2.3 + 2\(^3\).3 + ... + 2\(^{19}\).3

A = 3.(2+ 2\(^3\) + ... + 2\(^{19}\))

A ⋮ 3 (đpcm)

c; A = 2 + \(2^2\) + 2\(^3\) + ... + 2\(^{20}\)

Xét dãy số: 1; 2; 3;...; 20

Dãy số trên có 20 số hạng:

Vì 20 : 4 = 5

Vậy nhóm 4 hạng tử của A thành một nhóm khi đó:

A = (2+ 2\(^2\) + 2\(^3\) + 2\(^4\)) + ... + (2\(^{17}+2^{18}+2^{19}+2^{20}\))

A = 2.(1 + 2 + 2\(^2\) + 2\(^3\)) + ... + 2\(^{17}\).(1 + 2 + 2\(^2\) + 2\(^3\))

A = (1+ 2 +2\(^2\) + 2\(^3\)).(2+ ...+ 2\(^{17}\))

A = (1 + 2 + 4 + 8).(2+ ...+ 2\(^{17}\))

A = (3+ 4 + 8).(2+ ...+ 2\(^{17}\))

A = (7 + 8)(2+ ...+ 2\(^{17}\))

A = 15.(2+ ...+ 2\(^{17}\))

A ⋮ 5(đpcm)