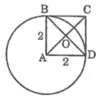
Cho điểm A nằm ngoài đường tròn (O; R). Vẽ các tiếp tuyến AB và AC với đường tròn
(O; R) (B, C là các tiếp điểm).
a) Chứng minh: OA L BC .b) Kể đường Kính BD của (O). Chứng minh: DC // OA.
c) Gọi H là giao điếm AO và BC, đường thăng AO căt đường tròn (O) lần lượt tại F và E sao cho AF nhỏ hơn AO. Chứng minh: HF.EA = FA.HE.






a: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra OA là đường trung trực của BC
=>OA⊥BC tại H và H là trung điểm của BC
b: Xét (O) có
ΔBCD nội tiếp
BD là đường kính
Do đó: ΔBCD vuông tại C
=>CB⊥CD
mà OA⊥BC
nên OA//CD
c: Ta có: \(\hat{FBA}+\hat{OBF}=\hat{OBA}=90^0\)
\(\hat{HBF}+\hat{OFB}=90^0\) (ΔBHF vuông tại H)
mà \(\hat{OBF}=\hat{OFB}\) (ΔOBF cân tại O)
nên \(\hat{FBA}=\hat{HBF}\)
=>BF là phân giác của góc HBA
Xét (O) có
ΔBFE nội tiếp
FE là đường kính
Do đó: ΔBFE vuông tại B
=>BF⊥BE
=>BE là phân giác ngoài tại đỉnh B của ΔHBA
Xét ΔHBA có BF là phân giác của góc HBA
nên \(\frac{FH}{FA}=\frac{BH}{BA}\left(3\right)\)
Xét ΔHBA có BE là phân giác ngoài tại đỉnh B
nên \(\frac{EH}{EA}=\frac{BH}{BA}\left(4\right)\)
Từ (3),(4) suy ra \(\frac{FH}{FA}=\frac{EH}{EA}\)
=>\(FH\cdot EA=FA\cdot EH\)