5.3^2-32:4^2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NK
19 tháng 12 2022
\(375:\left\{32-\left[4+\left(5.3^2-42\right)\right]\right\}\)
\(=375:\left\{32-\left[4+\left(45-42\right)\right]\right\}=375:\left\{32-\left[4+3\right]\right\}=375:\left\{32-7\right\}\)
=\(375:25=15\)
HM
2
YD
1
KV
23 tháng 10 2020
Đề em ghi bị thiếu dấu ngoặc nhé, sửa lại đề và giải như vầy:
375 : {32 - [4 + (5.32 - 42)]} - 14
= 375 : {32 - [4 + (5.9 - 42)]} - 14
= 375 : {32 - [4 + (45 - 42)]} - 14
= 375 : [32 - (4 + 3)] - 14
= 375 : (32 - 7) - 14
= 375 : 25 - 14
= 15 - 14
= 1
20 tháng 8 2019
a) \(142-\left[50-\left(2^3.10-2^3.5\right)\right]\)
= \(142-\left[50-\left(8.10-8.5\right)\right]\)
= \(142-\left[50-8.\left(10-5\right)\right]\)
= \(142-\left[50-8.5\right]\)
= \(142-\left[50-40\right]\)
= \(142-10\)
= \(132\)
b) \(375:\left\{32-\left[4+\left(5.3^2-42\right)\right]\right\}-14\)
= \(375:\left\{32-\left[4+\left(5.9-42\right)\right]\right\}-14\)
= \(375:\left\{32-\left[4+\left(45-42\right)\right]\right\}-14\)
= \(375:\left\{32-\left[4+3\right]\right\}-14\)
= \(375:\left\{32-7\right\}-14\)
= \(375:25-14\)
= \(15-14\)
= \(1\)
Chúc bạn học tốt !!!
20 tháng 8 2019
a) 142 - [ 50 - ( 23 . 10 - 23 . 5 )]
= 142 - [ 50 - ( 8 . 10 - 8 . 5 )]
= 142 - [ 50 - ( 80 - 40 )]
= 142 - [ 50 - 40 ]
= 142 - 10
= 132
b) 375 : { 32 - [ 4 + ( 5 . 32 - 42 )]} - 14
= 375 : { 32 - [ 4 + ( 5 . 9 - 42 )]} - 14
= 375 : { 32 - [ 4 + ( 45 - 42 )]} - 14
= 375 : { 32 - [ 4 + 3 ]} - 14
= 375 : { 32 - 7 } - 14
= 375 : 25 - 14
= 15 - 14
= 1
HT
4
12 tháng 7 2021
5.3x = 5.34
=> x = 4
5.34 = 7.35 - 2.35
= 35 . (7 - 2)
= 5. 35
=> 3x = 35
=> x = 5
RA
a) (2x-1)^3=27
b) (2x-1)^4=81
c) (x-2)^5=-32
d) (3x-1)^4=(3x-1)^6
đ) 5^x +5^x+2=650
g) 3^x-1 +5.3^x-1=162
6
26 tháng 8 2019
a) (2x-1)3 = 27
(2x-1)3 = 93
2x-1 = 9
2x = 9+1
2x = 10
x = 10:5
x = 2
Vậy x = 2
26 tháng 8 2019
b) (2x-1)4 = 81
(2x-1)4 = (\(\pm\)34)
2x-1 = \(\pm\)3
Trường hợp 1:
2x-1 = 3
2x = 3+1
2x = 4
x = 4:2
x = 2
Trường hợp 2:
2x-1 = -3
2x = -3+1
2x = -2
x = -2:2
x = -1
Vậy x \(\in[_{ }2;-1]\)
Vì không tìm thấy ngoặc nhọn nên mình dùng tạm ngoặc vuông nhé
MV
29 tháng 10 2017
\(A=\dfrac{12^{15}\cdot3^4-4^5\cdot3^9}{27^3\cdot2^{10}-32^3\cdot3^9}\\ =\dfrac{\left(2^2\cdot3\right)^{15}\cdot3^4-\left(2^2\right)^5\cdot3^9}{\left(3^3\right)^3\cdot2^{10}-\left(2^5\right)^3\cdot3^9}\\ =\dfrac{2^{30}\cdot3^{15}\cdot3^4-2^{10}\cdot3^9}{3^9\cdot2^{10}-2^{15}\cdot3^9}\\ =\dfrac{3^9\cdot2^{10}\left(2^{20}\cdot3^{10}\right)}{3^9\cdot2^{10}\left(1-2^5\right)}\\ =\dfrac{\left(2^2\right)^{10}\cdot3^{10}}{1-32}\\ =\dfrac{\left(2^2\cdot3\right)^{10}}{-31}\\ =\dfrac{-12^{10}}{31}\)
\(B=\dfrac{3}{1^2\cdot2^2}+\dfrac{5}{2^2\cdot3^2}+...+\dfrac{99}{49^2\cdot50^2}\\ =\dfrac{2^2-1^2}{1^2\cdot2^2}+\dfrac{3^2-2^2}{2^2\cdot3^2}+...+\dfrac{50^2-49^2}{49^2\cdot50^2}\\ =\dfrac{1}{1^2}-\dfrac{1}{2^2}+\dfrac{1}{2^2}-\dfrac{1}{3^2}+...+\dfrac{1}{49^2}-\dfrac{1}{50^2}\\ =1-\dfrac{1}{2500}\\ =\dfrac{2499}{2500}\)
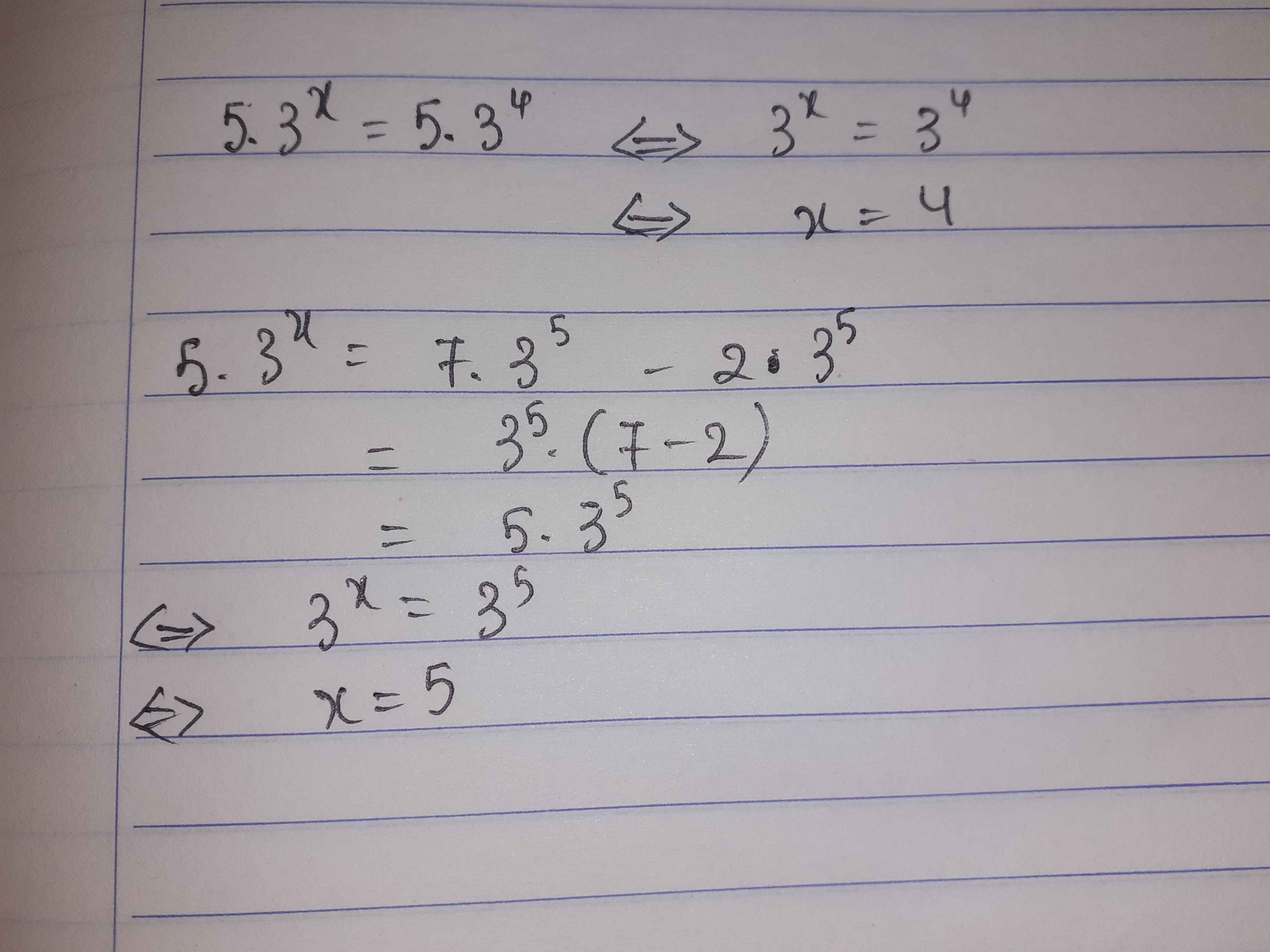
\(5.3^2-32:4^2=5.9-32:16\)
\(=45-2=43\)
\(5.3^2-32:4^2\)
\(=5.9-32:16\)
\(=45-2\)
\(=43\)