tìm góc song song và gthic vì sao
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
DN
1
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
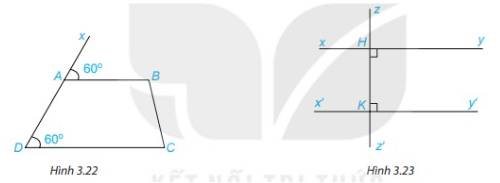
1. Vì \(\widehat {BAx} = \widehat {CDA}( = 60^\circ )\)
Mà 2 góc này ở vị trí đồng vị
\( \Rightarrow \) AB//CD (Dấu hiệu nhận biết hai đường thẳng song song)
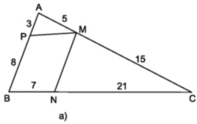
2. Ta có: \(\widehat {zKy'} + \widehat {y'Kz'} = 180^\circ \) ( 2 góc kề bù)
\(\begin{array}{l} \Rightarrow 90^\circ + \widehat {y'Kz'} = 180^\circ \\ \Rightarrow \widehat {y'Kz'} = 180^\circ - 90^\circ = 90^\circ \end{array}\)
Vì \(\widehat {yHz'} = \widehat {y'Kz'}\)
Mà 2 góc này ở vị trí đồng vị
\( \Rightarrow \) xy // x’y’ (Dấu hiệu nhận biết hai đường thẳng song song)
Chú ý:
2 đường thẳng cùng vuông góc với 1 đường thẳng thứ ba thì 2 đường thẳng đó song song.
CM
7 tháng 3 2019
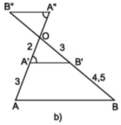
a) Xét hình 13a) : MN // AB.
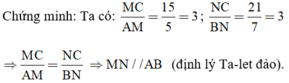
⇒ MN // AB (Theo định lý Ta-let đảo).
b) Xét hình 13b) : AB // A’B’ // A”B”.
Ta có: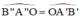 
⇒ A’B’ // A”B” (Hai góc so le trong bằng nhau).
Lại có:
CM
8 tháng 6 2018
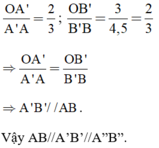
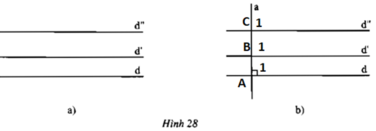
Vì a vuông góc với d ⇒ ∠A1 = 90o
• a có vuông góc với d’
Vì d//d’ ⇒ ∠A1 = ∠B1 ( hai góc đồng vị)
⇒ ∠B1 = 90o
• a có vuông góc với d’’
Vì d//d’’ ⇒ ∠A1 = ∠C1 (hai góc đồng vị)
⇒∠C1 = 90o
• d’ có song song với d’’
Vì ∠B1 = ∠C1 = 90o mà hai góc ở vị trí đồng vị
28 tháng 4 2015
a) vì hai tia Oy và Az cùng vuông góc với Ox nên chúng song song ( theo tính chất đường vuông góc)
b) vì góc xAz=góc xOy =90độ nên phân giác của chúng cũng bằng nhau và bằng 45 độ
nên ta có góc yOz=góc zAn (1)
mà Az // Oy nên góc yOz = góc AzO ( hai góc so le trong) (2)
từ 1 và 2 ta có góc AzO= góc nAz vì đây là hai góc so le trong nên suy ra nA//Om
6 tháng 9 2017
Cho góc vuông xOy điểm A ∈ tia Ox, kẻ tia Az vuông góc với Ox (tia Az nằm trong góc xOy)
a) Vì sao Oy // Az
b) Gọi Om là tia phân giác của góc xOy. An là tia phân giác của góc xAz. Vì sao Om // An
(Dấu hiệu nhận biết hai đường thẳng song song)
----------------------------
theo bài ra ta có:
góc xOy = 90 độ
Mà vì Az vuông góc với Ox (gt)
=> góc xAz = 90 độ
Mặt khác, góc xAz và góc xOy ở vị trí đồng vị
=> Az // Oy
=> đpcm
NT
2
7 tháng 7 2023
Nếu \(c\) vuông góc với đường thẳng \(a\) và \(b\) thì 2 góc so le sẽ bằng nhau (\(=90^o\)).
Vậy \(a//b\)
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
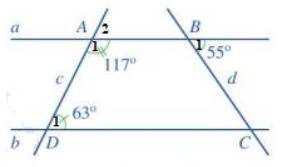
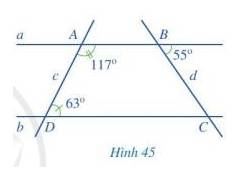
a) Vì \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) ( 2 góc kề bù) nên \(117^\circ + \widehat {{A_2}} = 180^\circ \Rightarrow \widehat {{A_2}} = 180^\circ - 117^\circ = 63^\circ \)
Vì \(\widehat {{A_2}} = \widehat {{D_1}}\) ( cùng bằng 63 độ)
Mà 2 góc này ở vị trí đồng vị
\( \Rightarrow \) a // b (Dấu hiệu nhận biết hai đường thẳng song song) ( đpcm)
b) Vì a // b nên \(\widehat {{B_1}} = \widehat {BCD}\) ( 2 góc so le trong), mà \(\widehat {{B_1}} = 55^\circ \Rightarrow \widehat {BCD} = 55^\circ \)
Hình 1: ta có: \(\hat{NAI}=\hat{AID}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AN//DH
Ta có: \(\hat{AID}=\hat{AKM}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên DH//MK
Ta có: AN//DH
DH//MK
Do đó: AN//DH//MK
Hình 2:
Ta có: \(\hat{N}+\hat{H}=70^0+110^0=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên MN//HK