x/2 - y/4 =1
x/3 + y/2 = -1
Giải hệ phương trình có phân số này sao vậy mn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 11 2017
Từ PT (1) ta có: y = (a + 1)x – (a + 1) (*)
Thế vào PT (2) ta được:
x + (a – 1) [(a + 1)x – (a + 1)] = 2 ⇔ x + ( a 2 – 1 ) x – ( a 2 – 1 ) = 2 x + (a2 – 1)x – (a2 – 1) = 2
⇔ a 2 x = a 2 + 1 ( 3 )
Với a ≠ 0 , phương trình (3) có nghiệm duy nhất x = a 2 + 1 a 2 . Thay vào (*) ta có:
y = a + 1 a 2 + 1 a 2 − a + 1 = a + 1 a 2 + 1 − a 2 a + 1 a 2 = a 3 + a + a 2 + 1 − a 3 − a 2 a 2 = a + 1 a 2
Suy ra hệ phương trình đã cho có nghiệm duy nhất ( x ; y ) = a 2 + 1 a 2 ; a + 1 a 2
⇒ x + y = a 2 + 1 a 2 + a + 1 a 2 = a 2 + a + 2 a 2
Đáp án: A
CM
4 tháng 11 2019
Từ PT (1) ta có: y = (a + 1)x – (a + 1) (*) thế vào PT (2) ta được:
x + ( a – 1 ) [ ( a + 1 ) x – ( a + 1 ) ] = 2 x + ( a 2 – 1 ) x – ( a 2 – 1 ) = 2
⇔ a 2 x = a 2 + 1 ( 3 )
Với a ≠ 0, phương trình (3) có nghiệm duy nhất x = a 2 + 1 a 2 . Thay vào (*) ta có:
y = ( a + 1 ) a 2 + 1 a 2 − ( a + 1 ) = a + 1 a 2 + 1 − a 2 a 2 + 1 a 2 = a 3 + a + a 2 + 1 − a 3 − a 2 a 2 = a + 1 a 2
Suy ra hệ phương trình đã cho có nghiệm duy nhất ( x ; y ) = a 2 + 1 a 2 ; a + 1 a 2
Hệ phương trình có nghiệm nguyên: x ∈ ℤ y ∈ ℤ ⇔ a 2 + 1 a 2 ∈ ℤ a + 1 a 2 ∈ ℤ ( a ∈ ℤ )
Điều kiện cần: x = a 2 + 1 a 2 = 1 + 1 a 2 ∈ ℤ ⇔ 1 a 2 ∈ ℤ mà a 2 > 0 ⇒ a 2 = 1
⇔ a = ± 1 ( T M a ≠ 0 )
Điều kiện đủ:
a = −1 ⇒ y = 0 (nhận)
a = 1 ⇒ y = 2 (nhận)
Vậy a = ± 1 hệ phương trình đã cho có nghiệm nguyên.
Đáp án: D
LA
6 tháng 1 2018
abc=100a+10b+c=n2-1(*)
cba=100c+10b+a=n2-4n+4(**)
(*)-(**)=99(a-c)=4n+5
=> 4n-5 chia hết cho 99
Mà \(100\le abc\le999\)
=> \(100\le n^2-1\le999\)
<=> \(101\le n^2\le1000\)=\(11< 31\)=\(39\le4n-5\le199\)
Vì 4n+5 chia hết cho 99
Nên 4n-5=99
4n=99+5
4n=104
n=104:4
n=26
Vậy abc=675
CM
6 tháng 4 2017
a) Điều kiện x ≥ 1; y ≥ 1.
Đặt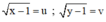 
(u, v ≥ 0).
Hệ phương trình trở thành:
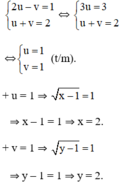
Vậy hệ phương trình có nghiệm (2; 2).
b) Đặt ( x – 1 ) 2 = u , u ≥ 0.
Hệ phương trình trở thành:
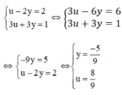
Vậy hệ phương trình có hai nghiệm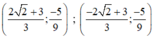 
CM
6 tháng 9 2019
Cách 1
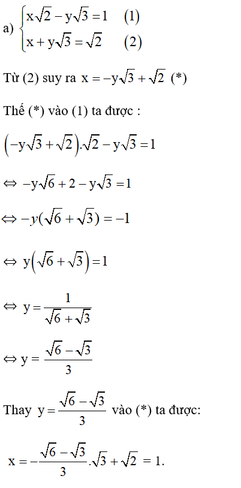
Vậy hệ phương trình có nghiệm duy nhất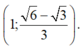 
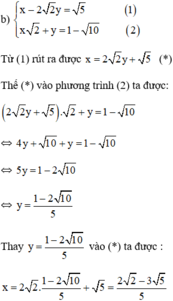
Vậy hệ phương trình có nghiệm duy nhất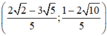 
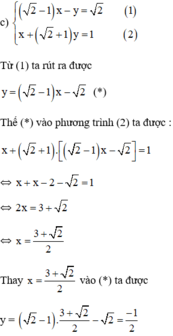
Vậy hệ phương trình có nghiệm duy nhất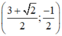 
Cách 2
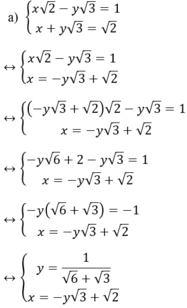
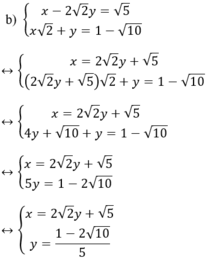
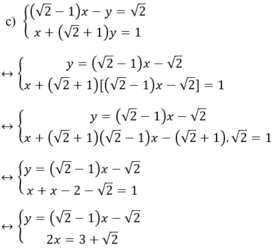
Kiến thức áp dụng
Giải hệ phương trình ta làm như sau:
Bước 1: Bước 1: Từ một phương trình (coi là phương trình thứ nhất), ta biểu diễn x theo y (hoặc y theo x) ta được phương trình (*). Sau đó, ta thế (*) vào phương trình thứ hai để được một phương trình mới ( chỉ còn một ẩn).
Bước 2: Dùng phương trình mới ấy thay thế cho phương trình thứ hai, phương trình (*) thay thế cho phương trình thứ nhất của hệ ta được hệ phương trình mới tương đương .
Bước 3: Giải hệ phương trình mới ta tìm được nghiệm của hệ phương trình.
CM
7 tháng 2 2017
a) Điều kiện x ≥ 1; y ≥ 1.
Đặt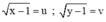 
(u, v ≥ 0).
Hệ phương trình trở thành:
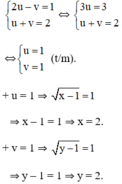
Vậy hệ phương trình có nghiệm (2; 2).
b) Đặt (x – 1)2 = u, u ≥ 0.
Hệ phương trình trở thành:
u − 2 y = 2 3 u + 3 y = 1 ⇔ 3 u − 6 y = 6 3 u + 3 y = 1 ⇔ − 9 y = 5 u − 2 y = 2 ⇔ y = − 5 9 u = 8 9 + u = 8 9 ⇒ ( x − 1 ) 2 = 8 9 ⇔ x − 1 = 2 2 3 x − 1 = − 2 2 3 ⇔ x = 2 2 + 3 3 x = − 2 2 + 3 3
Vậy hệ phương trình có hai nghiệm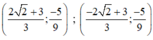 
CM
9 tháng 6 2017
Ta có
3 x − y = 2 m + 1 x + 2 y = − m + 2 ⇔ 6 x − 2 y = 4 m + 2 x + 2 y = − m + 2 ⇔ 7 x = 3 m + 4 x + 2 y = − m + 2 ⇔ x = 3 m + 4 7 3 m + 4 7 + 2 y = − m + 2 ⇔ x = 3 m + 4 7 2 y = − 7 m + 14 7 − 3 m + 4 7 ⇔ x = 3 m + 4 7 y = − 5 m + 5 7
hệ phương trình có nghiệm duy nhất ( x ; y ) = 3 m + 4 7 ; − 5 m + 5 7
Để x – y = 1 thì 3 m + 4 7 − − 5 m + 5 7 = 1 ⇔ 8m – 1 = 7 ⇔ 8m = 8 m = 1
Vậy với m = 1 thì hệ phương trình có nghiệm duy nhất (x; y) thỏa mãn x − y = 1
Đáp án: C
15 tháng 6 2023
1:
\(\left\{{}\begin{matrix}\dfrac{2x+1}{x+1}+\dfrac{3y}{y-1}=1\\\dfrac{3x}{x+1}-\dfrac{4y}{y-1}=10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2-\dfrac{1}{x+1}+3+\dfrac{3}{y-1}=1\\3-\dfrac{3}{x+1}-\dfrac{4y-4+4}{y-1}=10\end{matrix}\right.\)
=>-1/(x+1)+3/(y-1)=1-2-3=-5 và -3/(x+1)-4/(y-1)=10-3-4=3
=>x+1=13/11 và y-1=-13/18
=>x=2/11 và y=5/18
https://chatgpt.com/c/689b025a-26b8-832f-a874-60244db0553f
bn vào chưa