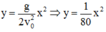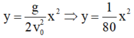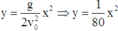Trong hệ trục tọa độ Oxy, cho 2 điểm A, B lần lượt di chuyển trên các trục Ox, Oy sao cho độ dài \(AB=l\left(l>0\right)\) không đổi. Phép vị tự tâm A, tỉ số \(k\) biến B thành M. Xác định quỹ tích của điểm M khi A và B di chuyển và viết phương trình của quỹ tích đó.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 8 2021
gọi Pt đường thảng .....y=ax+b(d)
d đi qua M(-1,1) 1=-a+b⇔b=a+1
gọi d cắt Ox tại \(A\left(-\dfrac{b}{a},O\right)\)
d cắt Oy tại \(B\left(O,b\right)\)
\(\Delta AOB\) vuông cân tại o
\(\Rightarrow OA=OB\Rightarrow\left(-\dfrac{b}{a}\right)^2+o^2=o^2+b^2\)
\(\dfrac{b^2}{a^2}=b^2\Leftrightarrow\dfrac{1}{a^2}=1\Leftrightarrow a^2=1\)
\(\Leftrightarrow\left[{}\begin{matrix}a=1\\a=-1\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}b=2\\b=0\left(loại\right)\end{matrix}\right.\)
(do d cắt 2 trục tọa độ nên a,b≠0)
vậy PtT đg thảng d:y=x+2
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 8 2021
Gọi pt đường thẳng có dạng \(y=ax+b\)
Đường thẳng qua M tạo 2 trục tọa độ 1 tam giác vuông cân khi nó có hệ số góc \(a=1\) hoặc \(a=-1\)
\(\Rightarrow\left[{}\begin{matrix}y=x+b\\y=-x+b\end{matrix}\right.\)
Thay tọa độ M vào phương trình ta được:
\(\left[{}\begin{matrix}1=-1+b\\1=-\left(-1\right)+b\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}b=2\\b=0\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}y=x+2\\y=-x\end{matrix}\right.\)
VT
8 tháng 2 2017
Chọn đáp án C.
Chuyển động ném ngang, theo phương Ox chất điểm chuyển động tahwngr đều, theo phương Oy chất điểm rơi tự do.
VT
27 tháng 12 2017
Chọn C
Chuyển động ném ngang, theo phương Ox chất điểm chuyển động tahwngr đều, theo phương Oy chất điểm rơi tự do
CM
31 tháng 5 2019
Phương trình elip có dạng:
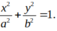
Đi qua hai điểm M; N ta được:
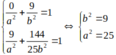
Vậy phương trình elip:
Chọn B.
