K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 5 2017
a) \(\left(P\Rightarrow Q\right):\)"Nếu \(x\) là một số hữu tỉ \(x^2\) cũng là một số hữu tỉ". Mệnh đề đúng.
b) Mệnh đề đảo là " Nếu \(x^2\) là một số hữu tỉ thì \(x\) là một số hữu tỉ"
c) Chẳng hạn, với \(x=\sqrt{2}\) mệnh đề này sai
PT
1
CM
27 tháng 10 2018
Mệnh đề “√2 là số hữu tỉ’’ sai vì √2 là số vô tỉ
Mệnh đề phủ định: "√2 không phải là một số hữu tỉ"
CM
15 tháng 1 2018
Mệnh đề phủ định của P: P− “ π không là một số hữu tỉ”.
P là mệnh đề sai, P− là mệnh đề đúng.
Mệnh đề phủ định của Q: Q− “Tổng hai cạnh của một tam giác nhỏ hơn hoặc bằng cạnh thứ ba”.
Q là mệnh đề đúng, Q− là mệnh đề sai.
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
+) Mệnh đề phủ định của mệnh đề P là \(\overline P \): “5,15 không phải là một số hữu tỉ”
Mệnh đề P đúng, \(\overline P \) sai vì \(5,15 = \frac{{103}}{{20}} \in \mathbb{Q}\), là một số hữu tỉ.
+) Mệnh đề phủ định của mệnh đề Q là \(\overline Q \): “2 023 không phải là số chẵn” (hoặc “2 023 là số lẻ”)
Mệnh đề Q sai, \(\overline Q \) đúng vì 2 023 có chữ số tận cùng là \(3 \ne \left\{ {0;2;4;6;8} \right\}\), đo đó 2 023 không phải là số chẵn.
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
23 tháng 9 2023
P: đúng
phủ định: "5,15 không phải số hữu tỉ"
Q: sai
Phủ định: "1023 không phải số chẵn"
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
a) Với n = 32, ta có các mệnh đề P, Q khi đó là:
P: “Số tự nhiên 32 chia hết cho 16”;
Q: “Số tự nhiên 32 chia hết cho 8”;
Mệnh đề P ⇒ Q: “Nếu số tự nhiên 32 chia hết cho 16 thì số tự nhiên 32 chia hết cho 8”.
Đây là mệnh đề đúng vì 32 chia hết cho 16 và 8.
b) Với n = 40, ta có các mệnh đề P, Q khi đó là:
P: “Số tự nhiên 40 chia hết cho 16”;
Q: “Số tự nhiên 40 chia hết cho 8”;
Mệnh đề đảo của mệnh đề P ⇒ Q là mệnh đề Q ⇒ P: “Nếu số tự nhiên 40 chia hết cho 8 thì số tự nhiên 40 chia hết cho 16”.
Mệnh đề đảo này là mệnh đề sai. Vì 40 chia hết cho 8 nhưng 40 không chia hết cho 16.
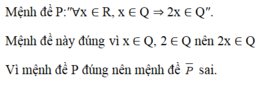
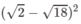
`a)` Ta có:
`a^2>=0` với mọi `a`
`->a^2>0` khi và chỉ khi `a\ne0`
Mà: `a<0->a\ne0`
Suy ra: `a^2>0` luôn đúng với khi `a<0`
`->` Đúng
`b)` Ta có:
`a^2>0` với mọi `a\ne0`
Nếu `a<0` thì `a^2>0`
Nếu `a>0` thì `a^2>0`
`->a^2>0` thì `a<0` hoặc `a>0`
`->` Sai
`c)` Ta có: `a^2>a`
`->a^2-a>0`
`->a(a-1)>0`
`->a>0` và `a-1>0` hoặc `a<0` và `a-1<0`
`->a>1` hoặc `a<0`
Suy ra nếu `a<0` thì `a^2>a`
`->` Đúng
`d)` Dựa theo câu `c)a^2>a` thì `a>1` hoặc `a<0`
`->a^2>a` thì chưa chắc `a>0`
`->` Sai
`e)` Dựa theo câu `c)a^2>a` thì `a>1` hoặc `a<0`
Do đó: `a^2>a` thì `a<0` là chưa đủ phải có thêm `a>1`
`->` Sai
Các câu đúng với mọi số hữu tỉ a là a,c