K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
MH
4
Những câu hỏi liên quan
CM
6 tháng 10 2019
Đường cao hình chóp bằng: 13 2 - 5 2 = 144 = 12 cm
Diện tích đáy bằng:S = 10.10 = 100 ( c m 2 )
Thể tích hình chóp bằng : V=1/3 S.h=1/3 .100.12=400 ( c m 3 )
Diện tích xung quanh bằng: S x q = Pd = 10.2.13 = 260 ( c m 2 )
Diện tích toàn phần là : S T P = S x q + S đ á y = 260 + 100 = 360 ( c m 2 )
CM
20 tháng 6 2017
Đường cao hình chóp bằng: 5 2 - 3 2 = 25 - 9 = 16 = 4 cm
Diện tích đáy bằng:S = 6.6 = 36 ( c m 2 )
Thể tích hình chóp bằng : V=1/3 S.h=1/3 .36.4=48 ( c m 3 )
Diện tích xung quanh bằng: S x q = Pd=2.6.5=60 ( c m 2 )
Diện tích toàn phần là : S T P = S x q + S đ á y = 60 + 36 = 96 ( c m 2 )
J
28 tháng 5 2021
Trong các khẳng định dưới đây, khẳng định nào đúng?
| Trung đoạn của hình chóp đều là đường cao hạ từ đỉnh xuống mặt phẳng đáy. SAI | ||
| Diện tích toàn phần của hình chóp bằng tổng của diện tích xung quanh và hai lần diện tích đáy. SAI | ||
| Diện tích xung quanh của hình chóp bằng tích của nửa chu vi đáy và trung đoạn. ĐÚNG |
AH
Akai Haruma
Giáo viên
25 tháng 5 2022
Lời giải:
a. Diện tích đáy: $5.5=25$ (cm2)
Chiều cao mỗi hình mặt bên: $\sqrt{6^2+(5:2)^2}=6,5$ (cm)
Diện tích mỗi mặt bên: $6,5.5:2=16,25$ (cm2)
Diện tích toàn phần: $25+16,25=41,25$ (cm2)
b. Thể tích: $\frac{1}{3}.6.25=50$ (cm3)
CM
13 tháng 5 2019
Hình chóp tứ giác đều, cạnh đáy bằng 1m, chiếu cao hình chóp bằng 0,5m.
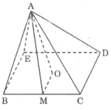
Tương tự hình vẽ câu a ta có AM Δ BC.
Vì AO là đường cao của hình chóp nên ΔAOM vuông tại O.
Áp dụng định li Pi-ta-go vào tam giác vuông AOM,ta có:
A M 2 = O A 2 + O M 2 = 0 , 5 2 + 0 , 5 2 = 0 , 5
Suy ra: AM = 0,5 cm
Ta có: S x q =1.2. 0 , 5 =2 0 , 5 ( m 2 )
S đ á y = 1.1=1( m 2 )
Vậy S T P = S x q + S đ á y = 2 0 , 5 + 1 ≈ 2,4( m 2 )
CM
14 tháng 11 2017
Hình chóp tứ giác đều cạnh đáy bằng 6cm, chiều cao hình chóp bằng 5cm.
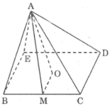
Tương tự hình vẽ câu a ta có MA Δ BC.
Vì AO là đường cao của hình chóp nên △ AOM vuông tại O.
Áp dụng định lí Pi-ta-go vào tam giác vuông AOM, ta có:
A M 2 = O A 2 + O M 2 = 25 + 9 = 34
Suy ra: AM = 34 cm
Ta có: S x q =6.2. 34 =12 34 ( c m 2 )
S đ á y = 6.6 = 36 ( c m 2 )
Vậy S T P = S x q + S đ á y = 12 34 +36 ≈ 106 ( c m 2 )
CM
11 tháng 2 2017
Hình chóp tứ giác đều, cạnh đáy bằng 20cm, chiều cao hình chóp bằng 7cm
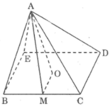
Tương tự hình vẽ câu a ta có MA Δ BC
Vì AO là đường cao của hình chóp nên ΔAOM vuông tại O.
Áp dụng định lí Pi-ta-go vào tam giác vuông AOM, ta có:
A M 2 = O A 2 + O M 2 = 49 + 100 = 149
Suy ra: AM = 149 cm
Ta có: S x q =20.2. 149 =40 149 ( c m 2 )
S đ á y = 20.20= 400( c m 2 )
Vậy S T P = S x q + S đ á y = 40 149 +400 ≈ 888,3( c m 2 )
PT
Tính diện tích toàn phần của các hình chóp đều sau đây: Hình chóp tứ giác đều OA = 8cm,BC = CD = 6cm
1
CM
23 tháng 3 2019
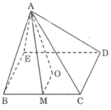
Vì AO là đường cao hình chóp nên ΔAOM vuông tại O.
Ta có OM = 1/2 CD = 3 (cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông AOM, ta có:
A M 2 = A O 2 + O M 2 = 8 2 + 3 2 = 73
Suy ra: AM = 73 (cm)
Ta có: S x q = Pd = 6.2. 73 = 12 73 ( c m 2 )
S đ á y = 6.6 = 36 ( c m 2 )
Vậy S T P = S x q + S đ á y = 12√73 +36 ≈ 138,5( c m 2 )
CM
12 tháng 2 2019
Diện tích xung quanh:
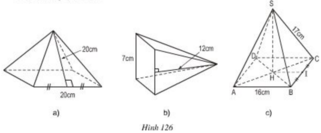
Hình a:
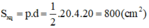
(trong đó chu vi đáy là 20.4 cm)
Diện tích đáy: Sd = 202 = 400 (cm2)
Diện tích toàn phần: Stp = Sxq + Sđ = 800 + 400 = 1200 (cm2)
Hình b:
Chu vi đáy là 4.7 = 28 (cm)
Diện tích xung quanh là:
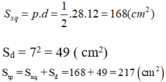
Hình c:
+) Diện tích đáy là Sd= 162 = 256 (cm2 ).
Do I là trung điểm của BC nên
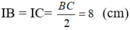
+) Tam giác SBC có SI là đường trung tuyến nên đồng thời là đường cao.
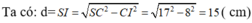
+) Chu vi đáy là: 16 .4 = 64 (cm)
+) Diện tích xung quanh là:
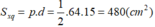
+) Diện tích toàn phần là:
Stp = Sđ + Sxq = 256 + 480 = 736 (cm2).
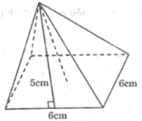
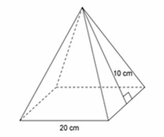
3 VÀ 4 CM
MẤY CÁI CẠNH Á CHỨ MÌNH KO BT TÍNH