bài này hơi khó
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
DB
9
Những câu hỏi liên quan
VS
4
MK
1
YN
20 tháng 6 2022
\(a)\)
\(A=\left(m-1\right)^3-\left(m-2\right)^3\)
\(=\left(m^3-3m^2+3m-1\right)-\left(m^3-6m^2+12m-8\right)\)
\(=m^3-3m^2+3m-1-m^3+6m^2-12m+8\)
\(=3m^2-9m+7\)
\(B=\left(3m-1\right)\left(3m+1\right)\)
\(=9m^2-1\)
\(\dfrac{1}{9}A=B-7\)
\(\Rightarrow\dfrac{1}{9}\left(3m^2-9m+7\right)=9m^2-1-7\)
\(\Rightarrow3m^2-9m+7=81m^2-72\)
\(\Rightarrow78m^2+9m-79=0\)
\(\Rightarrow m=\dfrac{-9\pm\sqrt{24729}}{156}\)
\(b)\)
\(A< B\)
\(\Rightarrow3m^2-9m+7< 9m^2-1\)
\(\Rightarrow6m^2+9m-8>0\)
\(\Rightarrow\left[{}\begin{matrix}m>\dfrac{-9+\sqrt{273}}{12}\\m< \dfrac{-9-\sqrt{273}}{12}\end{matrix}\right.\)
9 tháng 8 2023
uses crt;
var st,k,t:string;
d,dem,i:integer;
begin
clrscr;
readln(st);
d:=length(st);
k='';
dem=1;
for i:=2 to d do
begin
if st[i]=st[i-1] then inc(dem);
if st[i]<>st[i-1] then
btegin
str(dem,t);
if dem>1 then k:=k+t+st[i-1];
else k:=k+st[i-1];
dem=1;
end;
if (i=d) then
begin
str(dem,t);
if dem>1 then k:=k+t+st[i];
else k:=k+st[i];
end;
end;
write(k);
readln;
end.
28 tháng 4 2016
Gs có hữu hạn số nguyên tố
Chững minh điều hỉa sử đó là sai
Kết luận:k có hữu hạn số nguyên tố
22 tháng 7 2017
5/6 + 11/12 + 19/20 + ... + 89/90
= 1 - 1/6 + 1 - 1/12 + 1 - 1/20 + ... + 1-1/90
= [1+1+1+1...+1] - [1/2*3 + 1/3*4 + 1/4*5 + ... +1/9*10]
= 8 - [1/2 - 1/3 + 1/3 - 1/4 + 1/4 - 1/5 + ... + 1/9 - 1/10]
= 8 - [1/2 - 1/10]
= 8 - 2/5
= 38/5
22 tháng 7 2017
S=1-1/6+1-1/12+...+1-1/90
=8-(1/2.3+1/3.4+...+1/9.10)
=8-(1/2-1/3+1/3-1/4+...+1/9-1/10)
=8-(1/2-1/10)
=8-2/5
=38/5
VH
18 tháng 2 2017
= 156 đó bạn.ta chỉ cần lấy số lớn nhất - số bé nhất rồi chia khoảng cách x các số
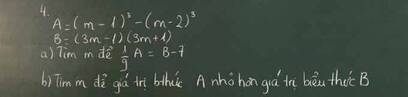
đúng
aaaaaaaaaaaaaaaaaaaaaaaaaaa