tìm hai số thực x,y biết x+y =4 và x.y=1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 10 2021
\(x-y=-30\Rightarrow\dfrac{x}{-30}=\dfrac{1}{y}\\ y.z=-42\\ \Rightarrow\dfrac{z}{-42}=\dfrac{1}{y}\\ \Rightarrow\dfrac{x}{-30}=\dfrac{z}{-42}\)
Áp dụng TCDTSBN ta có:
\(\dfrac{x}{-30}=\dfrac{z}{-42}=\dfrac{z-x}{-42-\left(-30\right)}=\dfrac{-12}{-12}=1\)
\(\dfrac{x}{-30}=1\Rightarrow x=-30\\ \dfrac{z}{-42}=1\Rightarrow z=-42\)
\(x.y=-30\Rightarrow-30.y=-30\Rightarrow y=1\)
11 tháng 12 2014
a, Do UCLN là 5 nên a, b chia hết cho 5 => tận cùng là 0 hoặc 5
Ta có 20 = 15 + 5 = 18 + 2=19+1=17+3=16+4=14+6=13+7=12+8=11+9
=> 2 số a và b là 15 và 5 hoặc 5 và 15
Bài sau làm tương tự em nhé :)
CA
3
28 tháng 1 2019
x + y = x . y
=> xy - x - y = 0
x ( y - 1 ) - ( y -1 ) = 0 +1
( x -1 ) ( y -1 ) = 1
ta có : 1 = 1 .1 = ( -1 ) . ( -1 )
T/H1 : x -1 = 1=> x = 2
=> y - 1 = 1 = > x =2
T/H2 : x -1 = -1 => x = 0
=> y -1 = -1 => y = 0
Vậy ( x ; y ) \(\in\){ ( 2 ; 2 ) ; ( 0 ; 0 }
28 tháng 1 2019
x+y - x+y =0
[x - xy]+y-1=-1
x.[1-y]-[-y+1]=-1
x.[1-y]-[1-y]=-1
[1-y] .[x-1]=-1
ta thay y thuoc z suy ra 1-y thuoc z
ta thay x thuoc z suy ra x-1 thuoc z
nen 1-y thuoc uoc cua -1
1-y thuoc 1 -1
ta co bang sau
1-y 1 -1
y 0 2
x-1 -1 1
x 0 2
PT
1
CM
28 tháng 10 2019
- Đặt (x; y) = d nên x = d.m; y = d.n với (m;n) =1. Giả sử x ≤ y thì m ≤ n.
- Ta có: x.y = dm.dn= d2.mn
BCNN(x; y) = x y x ; y = d 2 m . n d = d . m . n
- Ta có: BCNN (x;y) = 10 và x. y = 20 nên d = x y B C N N ( x ; y ) = 20 10 = 2
=> 2.m.n =10 nên m.n = 5
Bảng giá trị
20 tháng 10 2021
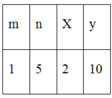
Bài 2:
Đặt \(\dfrac{x}{3}=\dfrac{y}{4}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3k\\y=4k\end{matrix}\right.\)
Ta có: xy=12
\(\Leftrightarrow12k^2=12\)
\(\Leftrightarrow k^2=1\)
Trường hợp 1: k=1
\(\Leftrightarrow\left\{{}\begin{matrix}x=3k=3\\y=4k=4\end{matrix}\right.\)
Trường hợp 2: k=-1
\(\Leftrightarrow\left\{{}\begin{matrix}x=3k=-3\\y=4k=-4\end{matrix}\right.\)
NH
3
23 tháng 12 2016
Giải:
Đặt \(\frac{x}{2}=\frac{y}{5}=k\)
\(\Rightarrow x=2k,y=5k\)
Ta có: \(xy=10\)
\(\Rightarrow2k5k=10\)
\(\Rightarrow10k^2=10\)
\(\Rightarrow k^2=1\)
\(\Rightarrow k=\pm1\)
+) \(k=1\Rightarrow x=2;y=5\)
+) \(k=-1\Rightarrow x=-2;y=-5\)
Vậy cặp số \(\left(x;y\right)\) là \(\left(2;5\right);\left(-2;-5\right)\)
24 tháng 1 2021
a, \(xy=5\)hay \(x;y\inƯ\left(5\right)=\left\{\pm1;\pm5\right\}\)
| x | 1 | -1 | 5 | -5 |
| y | 5 | -5 | 1 | -1 |
c, \(\left(x+1\right)\left(y-5\right)=-5\)hay \(x+1;y-5\inƯ\left(-5\right)=\left\{\pm1;\pm5\right\}\)
tự lập bảng, tương tự với mấy bài khác chỉ khác nó có điều kiện thì xét nó rồi kết luận nhé!
DK
0
F
1
30 tháng 10 2018
\(ƯCLN\left(x;y\right)=\frac{xy}{BCNN\left(x;y\right)}=\frac{20}{10}=2\)
Đặt \(x=2k,y=2t\) (y và t là 2 số nguyên tố cùng nhau)
\(xy=20\Rightarrow2k.2t=20\Rightarrow k.t=5\)
\(\Rightarrow k\inƯ\left(5\right)=\left\{1;5\right\}\)
\(\Rightarrow x=2k\in\left\{2;10\right\}\)
Nếu x = 2 thì y = 10
Nếu x = 10 thì y = 2
Vậy x = 2 và y = 10 hoặc x = 10 và y = 2
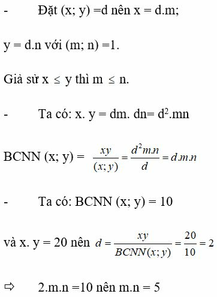
\(x+y\) = 4
\(x=4-y\)
Thay \(4-y\) vào biểu thức \(xy=1\)
Ta có: (4 - y).y = 1
4y - \(y^2\) = 1
-(y\(^2\) - 4y + 4) = - 3
(y - 2)\(^2\) = 3
\(\left[\begin{array}{l}y-2=\sqrt3\\ y-2=-\sqrt3\end{array}\right.\)
\(\left[\begin{array}{l}y=\sqrt3+2\\ y=-\sqrt3+2\end{array}\right.\)
\(\left[\begin{array}{l}x=4-\sqrt3-2\\ x=4+\sqrt3-2\end{array}\right.\)
\(\left[\begin{array}{l}x=\left(4-2\right)-\sqrt3\\ x=\left(4-2\right)+\sqrt3\end{array}\right.\)
\(\left[\begin{array}{l}x=2-\sqrt3\\ x=2+\sqrt3\end{array}\right.\)
Vậy: ...