cho hàm số y=x^3+3x-2
a, Tìm hệ số góc của t^2 của ĐTHS tại điểm M(1;3)
b, Viết PTTT của ĐTHS tại M
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 6 2021
2) Phương trình hoành độ giao điểm là:
3x+m=2x-1
\(\Leftrightarrow3x-2x=-1-m\)
\(\Leftrightarrow x=-m-1\)
Để (*) cắt đồ thị của hàm số y=2x-1 tại điểm nằm trên góc vuông phần tư thứ IV thì \(\left\{{}\begin{matrix}x>0\\y< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-m-1>0\\2x-1< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-m>1\\2\left(-m-1\right)-1< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< -1\\-2m-2-1< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< -1\\-2m< 3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< -1\\m>\dfrac{-3}{2}\end{matrix}\right.\Leftrightarrow-\dfrac{3}{2}< m< -1\)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 4 2022
a.
Do \(a=-2< 0\Rightarrow\)hàm số (1) đồng biến khi \(x< 0\)
b.
Phương trình hoành độ giao điểm:
\(-2x^2=-3x-5\Leftrightarrow2x^2-3x-5=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-1\Rightarrow y=-2\\x=\dfrac{5}{2}\Rightarrow y=-\dfrac{25}{2}\end{matrix}\right.\)
Hai đồ thị cắt nhau tại 2 điểm có tọa độ: \(\left(-1;-2\right)\) và \(\left(\dfrac{5}{2};-\dfrac{25}{2}\right)\)
18 tháng 11 2023
a: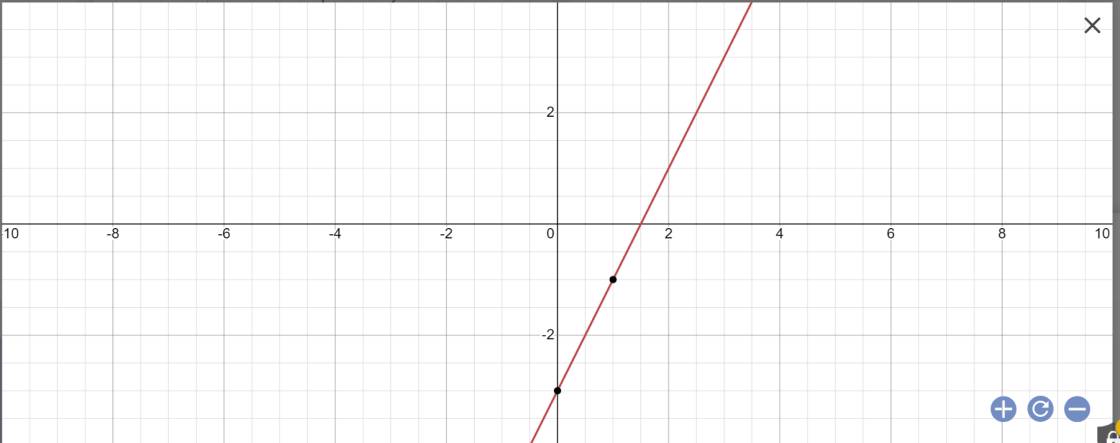 
b: Phương trình hoành độ giao điểm là:
\(2x-3=\dfrac{1}{2}x+3\)
=>\(2x-\dfrac{1}{2}x=3+3=6\)
=>\(\dfrac{3}{2}x=6\)
=>\(x=6:\dfrac{3}{2}=4\)
Thay x=4 vào y=2x-3, ta được:
\(y=2\cdot4-3=5\)
Vậy: M(4;5)
26 tháng 12 2021
\(a,\Leftrightarrow A\left(0;2\right)\in\left(d\right)\Leftrightarrow3m-1=2\Leftrightarrow m=1\\ b,\Leftrightarrow m-2=-2\Leftrightarrow m=0\\ c,\Leftrightarrow\left\{{}\begin{matrix}m-2=3\\3m-1\ne-2\end{matrix}\right.\Leftrightarrow m=5\\ d,\text{PT hoành độ giao điểm: }\left(m-2\right)x+3m-1=3x-2\\ \Leftrightarrow x\left(m-2-3\right)+3m-1+2=0\\ \Leftrightarrow x\left(m-5\right)=-3m-1\Leftrightarrow x=\dfrac{-3m-1}{m-5}\)
Vì 2 đt cắt bên trái trục tung nên hoành độ âm
\(\Leftrightarrow x< 0\Leftrightarrow\dfrac{-3m-1}{m-5}< 0\Leftrightarrow\dfrac{3m+1}{m-5}>0\Leftrightarrow\left[{}\begin{matrix}m>5\\m< -\dfrac{1}{3}\end{matrix}\right.\)
\(e,\text{Gọi điểm cố định mà }\left(d\right)\text{ luôn đi qua là }M\left(x_0;y_0\right)\\ \Leftrightarrow\left(m-2\right)x_0+3m-1=y_0\\ \Leftrightarrow mx_0-2x_0+3m-1-y_0=0\\ \Leftrightarrow m\left(x_0+3\right)-\left(2x_0+y_0+1\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}x_0+3=0\\2x_0+y_0+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=-3\\y_0=5\end{matrix}\right.\Leftrightarrow M\left(-3;5\right)\\ \text{Vậy }\left(d\right)\text{ luôn đi qua }M\left(-3;5\right)\)
17 tháng 12 2022
b: Vì (d) cắt y=-x+2 tại trục tung nên
a<>-1 và b=2
=>y=ax+2
Thay x=1 và y=3 vào y=ax+2, ta được:
a+2=3
=>a=1
c: Thay x=3y vào y=-x+2, ta được;
y=-3y+2
=>4y=2
=>y=1/2
=>B(3/2;1/2)
b: \(y=x^3+3x-2\)
=>\(y'=3x^2+3\)
\(y'\left(1\right)=3\cdot1^2+3=6\)
Phương trình tiếp tuyến là:
y-f(1)=f'(1)(x-1)
=>y-3=6(x-1)=6x-6
=>y=6x-6+3=6x-3