Tìm các giá trị của m để hs y=X3+ (m -1)x2+xm-2 ngịch biến trên khoảng (1;3)3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 6 2017
Đáp án D
Với y = ( m - 2 ) x 3 + ( m - 2 ) x 2 - x + 1 ta có y ' = 3 ( m - 2 ) x 2 + 2 ( m - 2 ) x - 1
Hàm số đã cho nghịch biến trên R
⇔ m - 2 < 0 ∆ ' ≤ 0 ⇔ m < 2 m 2 - m - 2 ≤ 0 ⇔ m < 2 - 1 ≤ m ≤ 2 ⇔ 1 ≤ m ≤ 2
CM
14 tháng 12 2019
Đáp án B
Phương pháp:
Hàm số y = f(x) nghịch biến trên (-∞;+∞) khi và chỉ khi f'(x) ≤ 0, ∀ x ∈ (-∞;+∞), f'(x) = 0 tại hữu hạn điểm.
Cách giải:
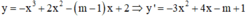
Hàm số đã cho nghịch biến trên khoảng (-∞;+∞)
CM
19 tháng 11 2018
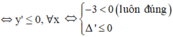
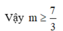
Chọn D.
Tập xác định: D = ℝ
Ta có 
Xét m = 1, ta có y' = -3 < 0 ∀ x ∈ ℝ nên nghịch biến trên tập xác định.
Xét m ≠ 1 Để hàm số trên nghịch biến trên tập xác định khi và chỉ khi
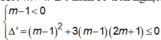
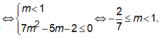
Vậy với - 2 7 ≤ m ≤ 1 thì hàm số y = ( m - 1 ) x 3 + ( m - 1 ) x 2 - ( 2 m + 1 ) + 5 nghịch biến trên tập xác định.
CM
20 tháng 7 2018
Đáp án là B.
Ta có y ' ( x ) = ( m - 1 ) x 2 - 2 ( m - 1 ) x - 1
TH1. m - 1 = 0 ⇔ m = 1 .Khi đó
y , = - 1 < 0 , ∀ x ∈ ℝ .Nên hàm só luôn nghịch biếến trên ℝ .
TH2. m - 1 ≢ 0 ⇔ m ≢ 1 .Hàm số luôn nghịch biến trên ℝ khi
y , ≤ 0 , ∀ x ∈ ℝ ⇔ ( m - 1 ) x 2 - 2 ( m - 1 ) x - 1 ≤ 0 , ∀ x ∈ ℝ ⇔ m - 1 < 0 ∆ ' ≤ 0 ⇔ m < 1 m ( m - 1 ) ≤ 0 ⇔ 0 ≤ m ≤ 1 . Kết hợp ta được 0 ≤ m < 1 .
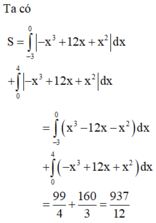
y
′
=g(x)=3x
2
−2(m+1)x−(2m
2
−3m+2)
Để hàm số đồng biến trên khoảng đã cho
⇔
𝑔
(
𝑥
)
≥
0
;
∀
𝑥
≥
2
⇔g(x)≥0;∀x≥2
Δ
′
=
(
𝑚
+
1
)
2
+
3
(
2
𝑚
2
−
3
𝑚
+
2
)
=
7
(
𝑚
−
1
2
)
2
+
21
4
>
0
;
∀
𝑚
Δ
′
=(m+1)
2
+3(2m
2
−3m+2)=7(m−
2
1
)
2
+
4
21
>0;∀m
⇒
⇒ Để
𝑔
(
𝑥
)
≥
0
;
∀
𝑥
≥
2
⇔
𝑥
1
<
𝑥
2
≤
2
g(x)≥0;∀x≥2⇔x
1
<x
2
≤2
⇔
{
(
𝑥
1
−
2
)
(
𝑥
2
−
2
)
≥
0
𝑥
1
+
𝑥
2
2
<
2
⇔{
(x
1
−2)(x
2
−2)≥0
2
x
1
+x
2
<2
⇔
{
𝑥
1
𝑥
2
−
2
(
𝑥
1
+
𝑥
2
)
+
4
≥
0
𝑥
1
+
𝑥
2
<
4
⇔{
x
1
x
2
−2(x
1
+x
2
)+4≥0
x
1
+x
2
<4
⇔
{
−
1
3
(
2
𝑚
2
−
3
𝑚
+
2
)
−
4
3
(
𝑚
+
1
)
+
4
≥
0
2
3
(
𝑚
+
1
)
<
4
⇔{
−
3
1
(2m
2
−3m+2)−
3
4
(m+1)+4≥0
3
2
(m+1)<4
⇔
{
−
2
𝑚
2
−
𝑚
+
6
≥
0
2
𝑚
<
10
⇔{
−2m
2
−m+6≥0
2m<10
⇒
−
2
≤
𝑚
≤
3
2
⇒−2≤m≤
2
3