x+2y+3z=92x−y+4z=83x+4y−z=3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
G
5 tháng 10 2018
Mình làm một câu để bạn tham khảo, sau đó bạn áp dụng làm các bài còn lại nha ^^
Có gì không hiểu bạn ib nha ^^
1. \(2x=3y-2x\left(1\right)\) và \(x+y=14\)
\(\left(1\right)\Leftrightarrow4x=3y\)
\(\Leftrightarrow\dfrac{x}{3}=\dfrac{y}{4}\)
Theo tính chất dãy tỉ số bằng nhau, có:
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{x+y}{3+4}=\dfrac{14}{7}=2\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2.3=6\\y=2.4=8\end{matrix}\right.\)
Bạn tự kết luận ^^
24 tháng 5 2022
3: 10x=6y=5z
\(\Leftrightarrow\dfrac{10x}{30}=\dfrac{6y}{30}=\dfrac{5z}{30}\)
hay x/3=y/5=z/6
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{6}=\dfrac{x+y-z}{3+5-6}=\dfrac{24}{2}=12\)
Do đó: x=36; y=60; z=72
4: Ta có: 9x=3y=2z
nên \(\dfrac{9x}{18}=\dfrac{3y}{18}=\dfrac{2z}{18}\)
hay x/2=y/6=z/9
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{6}=\dfrac{z}{9}=\dfrac{x-y+z}{2-6+9}=\dfrac{50}{5}=10\)
Do đó: x=20; y=60; z=90
20 tháng 9 2019
\(a,4x=5y\:\Rightarrow\frac{x}{5}=\frac{y}{4}\Rightarrow\frac{x}{15}=\frac{y}{12}\)
\(4y=6z\Rightarrow\frac{y}{6}=\frac{z}{4}\Rightarrow\frac{y}{12}=\frac{z}{8}\)
\(\Rightarrow\frac{x}{15}=\frac{y}{12}=\frac{z}{8}\)
\(\Rightarrow\frac{x}{15}=\frac{2y}{24}=\frac{3z}{24}\)
\(\Rightarrow\frac{x-2y+3z}{15-24+24}=\frac{x}{15}=\frac{y}{12}=\frac{z}{8}\)
\(\Rightarrow\frac{5}{15}=\frac{x}{15}=\frac{y}{12}=\frac{z}{8}\)
\(\Rightarrow\frac{1}{3}=\frac{x}{15}=\frac{y}{12}=\frac{z}{8}\)
\(\Rightarrow\hept{\begin{cases}x=\frac{1}{3}\cdot15=5\\y=\frac{1}{3}\cdot12=4\\z=\frac{1}{3}\cdot8=\frac{8}{3}\end{cases}}\)
CM
7 tháng 11 2019
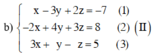
Đưa hệ phương trình về hệ dạng tam giác bằng cách khử dần ẩn số.
Nhân phương trình (1) với 2 rồi cộng với phương trình (2) và nhân phương trình (1) với (3) rồi trừ đi phương trình (3) ta được:
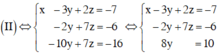
Giải hệ phương trình trên ta được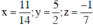 
Vậy hệ phương trình có nghiệm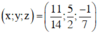 
24 tháng 7 2019
+) Áp dụng t/c của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{3}=\frac{y}{4}\Rightarrow\frac{x^2}{9}=\frac{y^2}{16}=\frac{x^2+y^2}{9+16}=\frac{100}{25}=4\)
=> \(\hept{\begin{cases}\frac{x^2}{9}=4\\\frac{y^2}{16}=4\end{cases}}\) => \(\hept{\begin{cases}x^2=4.9=36\\y^2=4.16=64\end{cases}}\) => \(\hept{\begin{cases}x=\pm6\\y=\pm8\end{cases}}\)
Vậy ...
5 tháng 4 2020
Đề câu g có vấn đề aa :>>>
Câu còn lại tương tự như trên mà
AN
24 tháng 12 2017
a, Bạn nghi sai đề: bài này mình làm rồi nên biết chỗ sai, nếu bạn nghi đúng đề thì mình làm sau nhé
\(\dfrac{2x-4y}{3}=\dfrac{4z-3x}{2}=\dfrac{3y-2z}{4}\)
=\(\dfrac{6x-12y}{9}=\dfrac{8z-6x}{4}=\dfrac{12y-8z}{16}\)
=\(\dfrac{6x-12y+8z-6x+12y-8z}{9+4+6}=\dfrac{0}{29}\)
Như vậy ta có thể suy ra
\(\Rightarrow\left\{{}\begin{matrix}2x=4y\Rightarrow\dfrac{x}{4}=\dfrac{y}{2}\\4z=3x\Rightarrow\dfrac{x}{4}=\dfrac{z}{3}\end{matrix}\right.\)
\(\Rightarrow\dfrac{x}{4}=\dfrac{y}{2}=\dfrac{z}{3}\)=\(\dfrac{2x-y+z}{8-2+3}=\dfrac{27}{9}=3\)
\(\dfrac{x}{4}=3\Rightarrow x=12\)
\(\dfrac{y}{2}=3\Rightarrow y=6\)
\(\dfrac{z}{3}=3\Rightarrow z=9\)
~~~~~~~~~~~~~~~~~~~~~~~~
AN
24 tháng 12 2017
b,
5x=8y=3z và x-2y+z= 34
Áp dụng tính chất của dãy tỉ số bằng nhau:
Ta có: 5x= 8y= 3z= \(\dfrac{5x}{120}=\dfrac{8y}{120}=\dfrac{3z}{120}=\dfrac{x}{24}=\dfrac{y}{15}=\dfrac{z}{40}\)
\(\Rightarrow\dfrac{x}{24}=\dfrac{y}{15}=\dfrac{z}{40}=\dfrac{x-2y+z}{24-30+40}=\dfrac{34}{34}=1\)
\(\dfrac{x}{24}=1\Rightarrow x=24\)
\(\dfrac{y}{15}=1\Rightarrow y=15\)
\(\dfrac{z}{40}=1\Rightarrow z=40\)
Còn 1 cách nữa nhưng thôi nha bạn
ko bt làm