tìm biểu thức :7 538 +6 542-8230 +26 139
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 10 2017
a) \(A=\frac{a^3+2a^2-1}{a^3+2a^2+2a+1}=\frac{\left(a^3+a^2\right)+\left(a^2-1\right)}{\left(a^3+1\right)+\left(2a^2+2a\right)}=\frac{a^2\left(a+1\right)+\left(a-1\right)\left(a+1\right)}{\left(a+1\right)\left(a^2-a+1\right)+2a\left(a+1\right)}\)
\(=\frac{\left(a+1\right)\left(a^2+a-1\right)}{\left(a+1\right)\left(a^2+a+1\right)}=\frac{a^2+a-1}{a^2+a+1}\)
Gọi d là \(ƯCLN\left(a^2+a-1;a^2+a+1\right)\) nên :
\(\hept{\begin{cases}a^2+a-1⋮d\\a^2+a+1⋮d\end{cases}}\) \(\Leftrightarrow\left(a^2+a+1\right)-\left(a^2+a-1\right)=2⋮d\Rightarrow d=\left\{\pm1;\pm2\right\}\)
Mà \(a^2+a+1=a\left(a+1\right)+1\) do \(a\left(a+1\right)\) là tích 2 số nguyên liên tiếp
=> \(a\left(a+1\right)⋮2\Rightarrow a\left(a+1\right)+1\) ko chia hết cho 2 hay \(d\ne\pm2\)
\(\Rightarrow d=\pm1\) hay \(\frac{a^2+a-1}{a^2+a+1}\) tối giản (đpcm)
A
4 tháng 2 2019
a. Ta có biến đổi:
\(A=\frac{a^3+2a^2-1}{a^3+2a^3+2a+1}\)
\(A=\frac{\left(a+1\right)\left(a^2+a-1\right)}{\left(a+1\right)\left(a^2+a+1\right)}\)
\(A=\frac{a^2+a-1}{a^2+a+1}\)
b. Gọi d là ước chung lớn nhất của \(a^2+a-1\)và \(a^2+a+1\)
Vì \(a^2+a-1=a\left(a+1\right)-1\)là số lẻ nên d là số lẻ
Mặt khác, \(2=\left[a^2+a+1-\left(a^2+a-1\right)\right]⋮d\)
Nên d = 1 tức là \(a^2+a+1\)và \(a^2+a-1\)nguyên tố cùng nhau.
Vậy biểu thức A là phân số tối giản.
sao cho 
PA
18 tháng 8 2016
\(A=\frac{a^3+2a^2-1}{a^3+2a^2+2a+1}=\frac{a^3+2a^2+2a+1-2a-2}{a^3+2a^2+2a+1}=\frac{a^3+2a^2+2a+1}{a^3+2a^2+2a+1}-\frac{2\left(a+1\right)}{a^3-a^2+a+a^2-a+1+2a^2+2a}\)
\(=1-\frac{2\left(a+1\right)}{a\left(a^2-a+1\right)+\left(a^2-a+1\right)+2a\left(a+1\right)}=1-\frac{2\left(a+1\right)}{\left(a+1\right)\left(a^2-a+1\right)+2a\left(a+1\right)}\)
\(=1-\frac{2\left(a+1\right)}{\left(a+1\right)\left(a^2-a+1+2a\right)}=1-\frac{2}{a^2+a+1}\)
- a lẻ => a2 + a + 1 lẻ => A tối giản
- a chẵn => a2 + a + 1 lẻ => A tối giản
PT
1
PT
1
CM
10 tháng 5 2017
a)267 + 125 - 278 = 392 - 278 = 114
b) 538 - 38 ´ 3 = 538 - 114 = 424
C
12 tháng 12 2023
a) 542 x 7 + 542 x 2 + 542
= 542 x 7 + 542 x 2 + 542 x 1
= 542 x (7 + 2 + 1)
= 542 x 10
= 5420
b) (126 x 35 + 157 x 55) x (132 - 6 x 22)
= (126 x 35 + 157 x 55) x (132 - 132)
= (126 x 35 + 157 x 55) x 0 (Số bất kỳ nào nhân với 0 vẫn = 0)
= 0
c) 897 x 99 + 897
= 897 x 99 + 897 x 1
= 897 x (99 + 1)
= 897 x 100
= 89700
12 tháng 12 2023
a) \(542.7+542.2+542\)
\(=542.\left(2+7+1\right)\)
\(=542.10=5420\)
b) \(\left(126.35+157.55\right).\left(132-6.22\right)\)
\(=13045.0=0\)
c) \(897.99+897\)
\(=897.\left(99+1\right)\)
\(=897.100=89700\)
8 tháng 12 2017
(139139 . 133 - 133133 . 139) : (2 + 4+ 6 + ... + 2002)
= (139 . 1001 . 133 - 133 . 1001 . 139) : (2 + 4 + 6 + ... + 2002)
= 0 : (2 + 4 + 6 + ... + 2002)
= 0
TQ
27 tháng 3 2020
a, ( 26 - 6) . (-4) + 31. (-7-13)
=20 . ( -4) + 31.(-20)
=(-80) + (-620)
= (-700)
b,4.(-5)^2 - 6.(26-21)
=4.25 - 6.5
= 100- 30
=70
c,56.(-24) + 24.(-44)
=(-1334)+(-1056)
= -2390
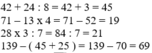
32034
31989