Cho tam giác ABC, vẽ BD ⊥ AC và CE ⊥ AB. CM: BD + CE < AB + AC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


3b)
Ta có tg BNK vuông tại K ->BN>BK
Ta có IK=MN(tính chất đoạn chắn)
Ta có : BC+MN=BK+KC+MN=BK+BI+IK=2BK
Vì BK<BN->2BK<2BN->BN>BK/2->BN>BC+MN/2

a) Xét tam giác vuông ABD và tam giác vuông ACE có
góc A: chung
=> tam giác ABD = tam giác ACE (cạnh huyền - góc nhọn)
=> BD=CE và AD=AE(hai cạnh tương ứng)
b) Vì AB=AC và AE=AD => AB-AE=AC-AD => BE=CD
Xét tam giác vuông OEB và tam giác vuông ODC có
BE=CD
góc BOE = góc COD (đối đỉnh)
=> tam giác OEB = tam giác ODC(cạnh góc vuông-góc nhọn kề cạnh) => OB=OC
c) Xét tam giác AOB và tam giác AOC có
AB=AC
OB=OC
AO: cạnh chung
=> tam giác AOB = tam giác AOC (c.c.c)
=> góc OAB=góc OAC(hai góc tương ứng)
=> AO la tia phân giác góc BAC

Dễ mà :
Gợi ý ta sẽ áp dụng hệ quả là : Trong một tam giác vuông thì Cạnh huyền luôn lớn hơn Cạnh góc vuông
Giải
B A E F D C
a , Xét \(\Delta BAD\)và \(\Delta BED\)có :
AB = BE ( gt )
BD chung
\(\widehat{ABD}=\widehat{DBE}\)( BD là đường phân giác \(\widehat{B}\))
\(\Rightarrow\text{}\text{}\text{}\text{}\text{}\text{}\Delta ABD=\Delta BDE\left(c.g.c\right)\)
b , Có \(\Delta ABD=\Delta BDE\)
\(\Rightarrow\widehat{E}=\widehat{A}=90^0\)( 2 góc tương ứng )
Ta có : \(\hept{\begin{cases}\widehat{AFD}+\widehat{ADF}=90^0\\\widehat{ECD}+\widehat{EDC}=90^0\\\widehat{ADF}=\widehat{EDC}\left(đđ\right)\end{cases}}\)
\(\Rightarrow\widehat{AFD}=\widehat{DCE}\)
Xét \(\Delta ADF\)vuông tại A và \(\Delta EDC\)vuông tại E có :
\(\hept{\begin{cases}\text{ AF = EC ( gt )}\\\widehat{AFD\: }=\widehat{DCE}\left(cmt\right)\end{cases}\Rightarrow\Delta ADF=\Delta EDC\left(cgv.gn\right)}\)
\(\Rightarrow DF=DC\)( 2 cạnh tương ứng )
c , Có \(D\in AC\)( BD cắt AC tại D )
\(\widehat{EDC}+\widehat{ADE}=180^0\)
Mà \(\widehat{ADF}=\widehat{EDC}\)( 2 góc đối đỉnh )
\(\Rightarrow\widehat{ADF}+\widehat{ADE}=180^0\)
\(\Rightarrow\widehat{EDF}=180^0\)
\(\Rightarrow\)E , D , F cùng nằm trên 1 đường thẳng .

a) Xét tam giác ABD và tam giác ACE có
góc ADB = góc AEC = 90 độ
AB=AC
góc A: chung
=> tam giác ABD = tam giác ACE (cạnh huyền - góc nhọn)
=> BD=CE và AD=AE
b) Vì AB=AC và AE=AD => AB-AE=AC-AD => BE=CD
Xét tam giác OEB và tam giác ODC có
góc OEB = góc ODC = 90 độ
BE=CD
góc BOE = góc COD (đối đỉnh)
=> tam giác OEB = tam giác ODC => OB=OC
c) Xét tam giác AOB và tam giác AOC có
AB=AC
OB=OC
AO: cạnh chung
=> tam giác AOB = tam giác AOC (c.c.c)
=> góc OAB=góc OAC
=> AO la tia phân giác góc BAC
Bài mk lm như dzị ak
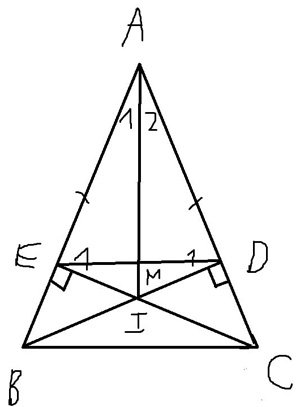
^E1 = ^D1 = 90 độ
AB = AC
^A chung
=> tg ADB = tg AEC
=> AD = AE
=> tg ADE cân
b, tg ABI và tg ACI có
^E1 = ^D1 = 90 độ
AI chung
AB = AC
=> tg ABI = tg ACI
=> ^A1 = ^A2 ( góc t/ứ)
=> IB = IC ( cạnh t/ứ)
=> tg IBC cân
c, vì ^A1 = ^A2 ( câu b )
=> AI là tpg của góc EAD

A B C E D GT cho AB lon hon AC
Suy ra góc ACB lơn hơn góc ABC[theo quan hệ góc và cạnh đối diện]
từ trên ta có BD lớn hơn EC [theo quan hệ góc và cạnh đối diện]

a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
góc BAD chung
=>ΔADB=ΔAEC
=>BD=CE
b: góc ABD=góc ACE
=>góc HBC=góc HCB
=>ΔHBC cân tại H
c: AB=AC
HB=HC
=>AH là trung trực của BC
Chứng minh bất đẳng thức: \(B D + C E < A B + A C\)
1. Phân tích bài toán
2. Chứng minh
Xét hai tam giác vuông \(B D A\) và \(C E A\):
\(B D < A B\)
Vì \(B D\) là đường cao và là cạnh góc vuông, còn \(A B\) là cạnh huyền trong tam giác vuông \(B D A\).
\(C E < A C\)
Vì \(C E\) là đường cao và là cạnh góc vuông, còn \(A C\) là cạnh huyền trong tam giác vuông \(C E A\).
Cộng hai bất đẳng thức trên:
\(B D + C E < A B + A C\)3. Kết luận
Vậy ta đã chứng minh được rằng:
\(B D + C E < A B + A C\) 4o