Cho hinh chóp SABCD đay hình vuông cạnh a
SA vuông (ABCD), SA= a. Tính
((SBD); ABCD)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HN
4 tháng 2 2022
Gọi H là hình chiếu của S lên mp(ABCD), suy ra H thuộc BD (ABCD là hình thoi, SA=SB=SC).
Ta có: SA=SC=BA=BC=3 cm, suy ra SO=BO, suy ra tam giác SBD là tam giác vuông (đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền).
0,5.SB.SD=6, suy ra SD=4 cm, suy ra BD=5 cm, AC=\(\sqrt{11}\) cm, SH=2,4 cm.
Thể tích cần tìm là V=1/3.2,4.0,5.5.\(\sqrt{11}\)=2\(\sqrt{11}\) (cm3).
CM
2 tháng 3 2017
a) Gọi O là tâm của hình thoi, ta có AC ⊥ BD tại O
Vì SA = SC nên SO ⊥ AC.
Do đó AC vuông góc với mặt phẳng (SBD)
Ta suy ra mặt phẳng (ABCD) vuông góc với mặt phẳng (SBD).
b) Ba tam giác SAC, BAC, DAC bằng nhau ( c.c.c) nên ta suy ra OS = OB = OD. Vậy tam giác SBD vuông tại S.
CM
30 tháng 8 2019
Đáp án là B
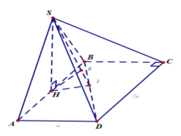
Gọi H là trung điểm của AB . Tam giác SAB đều nên suy ra SH ⊥AB . Theo giả thiết (SAB) vuông góc với ( ABCD) và có giao tuyến AB nên suy ra SH ⊥ (ABCD) tại H . Có AH ∩ (SBD) = B nên
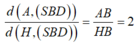
Trong ( ABCD) kẻ HI ⊥ BD tại I , kết hợp SH ⊥ (ABCD) ta suy ra
BD⊥ (SHI) => (SHI) ⊥ (SBD) , mà (SHI ) ∩ (SBD) = SI nên trong (SHI) nếu ta kẻ HK ⊥ SI tại K thì HK ⊥ (SBD) tại K , do đó HK = d (H,( SBD)) .
Ta tính được :
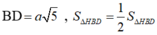
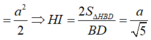
Tam giác SAB đều cạnh 2a nên SH=a 3
Tam giác SHI vuông tại H đường cao HK nên
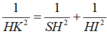
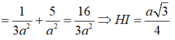
Vậy khoảng cách từ A đến (SBD) là: a 3 2
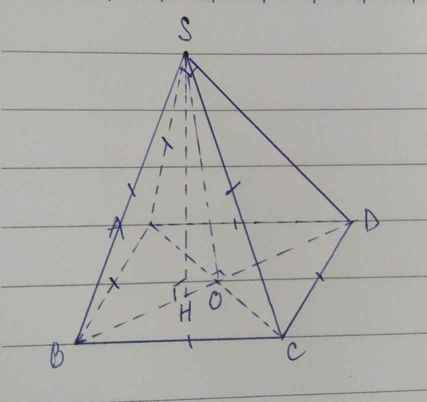
Gọi O là tâm của đáy ABCD
ABCD là hình vuông
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Ta có: BD⊥AC(ABCD là hình vuông)
BD⊥SA(SA⊥(ABCD))
SA,AC cùng thuộc mp(SAC)
Do đó: BD⊥(SAC)
=>BD⊥SO
(SBD) cắt (ABCD)=BD
SO⊥BD; SO⊂(SBD)
AC⊥BD; AC⊂(ABCD)
Do đó: góc giữa hai mp(SBD) và (ABCD) là góc giữa SO và AC
ΔSAO vuông tại A
=>\(\hat{SOA}<90^0\)
=>Góc giữa hai mp (SBD) và (ABCD) là \(\hat{SOA}\)
ABCD là hình vuông
=>\(CA^2=BA^2+BC^2=a^2+a^2=2a^2\)
=>\(CA=a\sqrt2\)
O là trung điểm của AC
=>\(AO=\frac{CA}{2}=\frac{a\sqrt2}{2}\)
Xét ΔSAO vuông tại A có \(\tan SOA=\frac{SA}{AO}=a:\frac{a\sqrt2}{2}=\frac{2}{\sqrt2}=\sqrt2\)
nên \(\hat{SOA}\) ≃55 độ
=>Góc giữa hai mp(SBD) và (ABCD) gần bằng 55 độ