cho A=\(\frac14+\frac19+\frac{1}{16}+\cdots+\frac{1}{2024^2}\) CMR A\(\le\frac34\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chứng minh rằng không thể biểu diễn số 11 thành tổng các nghịch đảo của bình phương của kk số tự nhiên khác nhau từng đôi một (k∈N,k⩾2k∈N,k⩾2)
GIẢI :
Xét 2 trường hợp :
+ Nếu trong k số tự nhiên đó có số 1 thì dĩ nhiên tổng đó lớn hơn 11^2=1
+ Nếu trong k số tự nhiên đó không có số 1 :
[tex]\frac{1}{n^2}< \frac{1}{(n-1).n}[/tex] |
[tex]\Rightarrow \frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{n^2}< \frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{(n-1).n}=\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{n-1}-\frac{1}{n}=1-\frac{1}{n}< 1[/tex] |
Vậy dù tổng ở vế trái có bao nhiêu số hạng thì nó vẫn nhỏ hơn 11.
Trong cả 2rường hợp, tổng các nghịch đảo của bình phương của k số tự nhiên khác nhau từng đôi một luôn luôn khác 1 (lớn hơn hoặc nhỏ hơn 1) ⇒⇒đpcm.

a. Gọi phân số cần tìm là \(\frac{a}{b}\)
\(\Rightarrow\) Phân số nghịch đảo là \(\frac{b}{a}\)
Theo bài ra, ta có:
\(\frac{a}{b}+\frac{b}{a}\ge2\)
\(\Leftrightarrow\frac{a^2+b^2}{ab}\ge2\)
\(\Leftrightarrow a^2+b^2\ge2ab\)
\(\Leftrightarrow a^2+b^2-2ab\ge0\)
\(\Leftrightarrow a^2-ab+b^2-ab\ge0\)
\(\Leftrightarrow a\left(a-b\right)+b\left(b-a\right)\ge0\)
\(\Leftrightarrow a\left(a-b\right)-b\left(a-b\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)\left(a-b\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)^2\ge0\)
Vì (a-b)2 chắc chắn lớn hơn hoặc bằng 0
\(\Rightarrow\frac{a}{b}+\frac{b}{a}\ge2\)
Vậy tổng của một phân số dương với ghịch đảo của nó luôn lớn hơn hoặc bằng 2.

uses crt;
var a:array[1..250]of integer;
i,n,dem,t,t1,t2,t3,t4:integer;
begin
clrscr;
repeat
write('Nhap n='); readln(n);
until (0<n) and (n<=250);
for i:=1 to n do
begin
repeat
write('A[',i,']='); readln(a[i]);
until (0<a[i]) and (a[i]<=500);
end;
dem:=0;
for i:=1 to n do
if a[i] mod 2=1 then inc(dem);
writeln('So phan tu co gia tri le la: ',dem);
t:=0;
for i:=1 to n do
if i mod 2=0 then t:=t+a[i];
writeln('Tong cac phan tu co chi so chan la: ',t);
t1:=0;
for i:=1 to n do
if i mod 2=1 then t1:=t1+a[i];
writeln('Tong cac phan tu co chi so le la: ',t1);
t2:=0;
for i:=1 to n do
if (i mod 2=0) and (a[i] mod 2=0) then t2:=t2+a[i];
writeln('Tong cac phan tu chan co chi so chan la: ',t2);
t3:=0;
for i:=1 to n do
if (i mod 2=1) and (a[i] mod 2=1) then t3:=t3+a[i];
writeln('Tong cac phan tu co chi so le la: ',t3);
t4:=0;
for i:=1 to n do
t4:=t4+a[i];
writeln('Trung binh cong cac so trong day la: ',t4/n:4:2);
readln;
end.

Gọi phân số dương là \(\dfrac{a}{b}\) và phân số nghịch đảo của nó là \(\dfrac{b}{a}\)
với điều kiện: a > 0; b > 0; a ≥ b
=> a = b + m (m ≥ 0)
Theo đề bài ta có:
\(\dfrac{a}{b}\) + \(\dfrac{b}{a}\) = \(\dfrac{b+m}{b}\) + \(\dfrac{b}{b+m}\) = 1 + \(\dfrac{m}{b}\) + \(\dfrac{b}{b+m}\) ≥ 1 + \(\dfrac{m}{b+m}\) + \(\dfrac{b}{b+m}\) = 1 + \(\dfrac{m+b}{m+b}\) = 2
=> \(\dfrac{a}{b}\) + \(\dfrac{b}{a}\) ≥ 2 (điều phải chứng minh)
_______________________________________________
Có gì không đúng nhắn mình nha bạn :))

Ta có: \(A=2+4+6+...+98+100\)
\(B=1+3+5+...+97+99\)
\(\Rightarrow A-B\)
\(=\left(2+4+6+...+100\right)-\left(1+3+5+7+...+99\right)\)
\(=\left(2-1\right)+\left(4-3\right)+...+\left(100-99\right)\)
\(=1+1+1+...+1\) (50 số 1)
\(=50\)

a)Năm số hạng đầu: 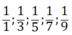
Số hạng tổng quát của dãy số: 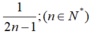
b)Năm số hạng đầu: 1;4;7;10;13
Số hạng tổng quát của dãy số: 3n + 1(n ∈ N)
bạn hỏi cô ý
nhưng mình cần gấp