Cho tam giác ABC vuông tại A.Tia phân giác của △ABC cắt AC tại E,trên cạnh BC lấy điểm D sao cho BD=BA
a)Chứng minh rằng:△ABE=△DBE,△AED là tam giác cân.
b)Tia DE cắt tia BA tại M,gọi H là giao điểm của AD và BE.Chứng minh rằng: DE>HD và DM>2DH.
c)Qua điểm D kẻ đường thẳng song song với BE cắt AC tại F.Gọi K là giao điểm của DE và HF.Chứng minh rằng KD=2KE

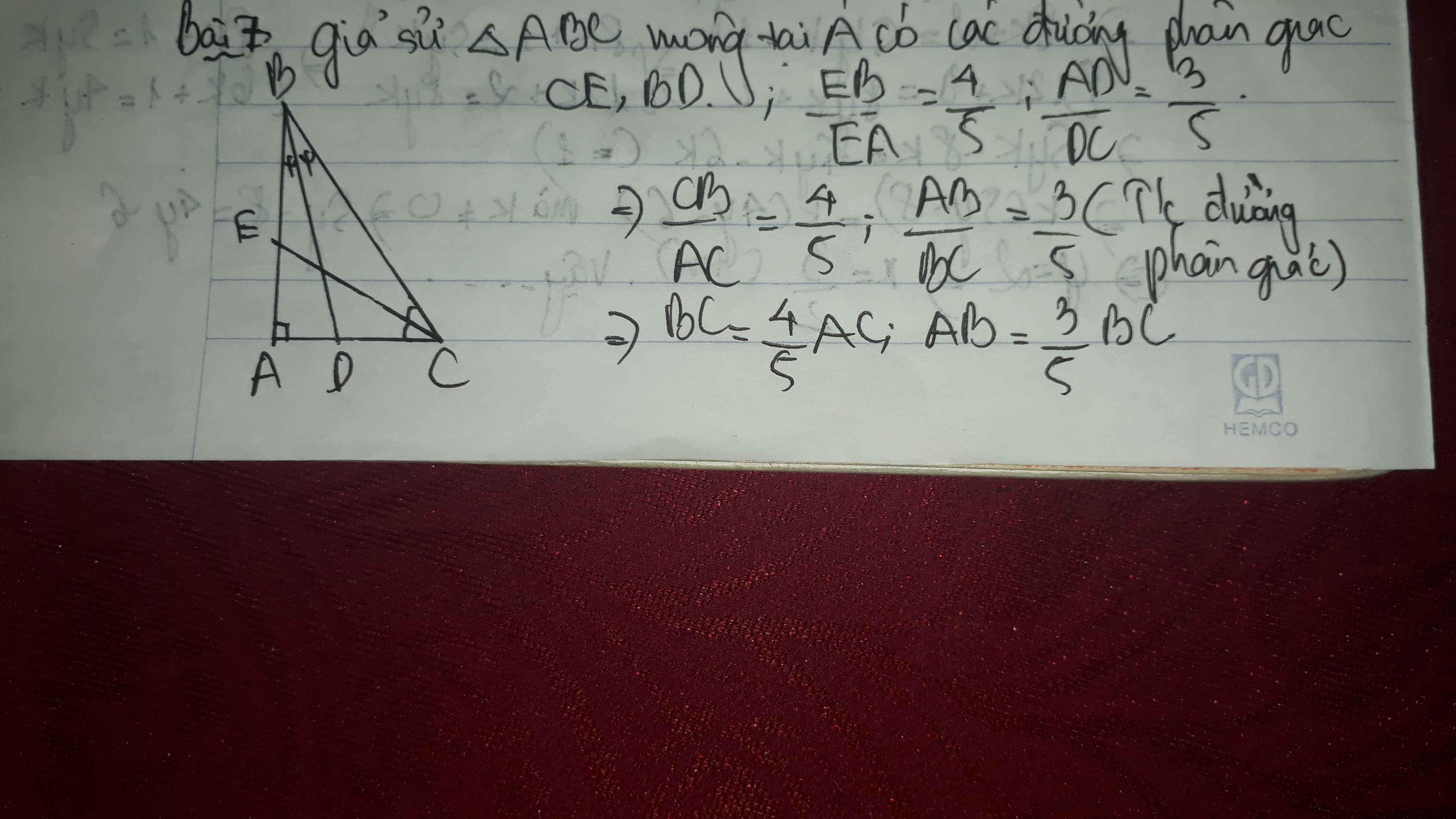


a: Xét ΔBAE và ΔBDE có
BA=BD
\(\widehat{ABE}=\widehat{DBE}\)
BE chung
Do đó: ΔBAE=ΔBDE
=>EA=ED
=>ΔEAD cân tại E
b: BA=BD
=>B nằm trên đường trung trực của AD(1)
Ta có: EA=ED
=>E nằm trên đường trung trực của AD(2)
Từ (1),(2) suy ra BE là đường trung trực của AD
=>BE\(\perp\)AD tại H và H là trung điểm của AD
ΔDHE vuông tại H
=>DE là cạnh huyền
=>DE là cạnh lớn nhất trong ΔDHE
=>DE>HD
\(\widehat{DAM}=\widehat{DAC}+\widehat{MAC}=90^0+\widehat{DAC}>90^0\)
Xét ΔDAM có \(\widehat{DAM}>90^0\)
nên DM là cạnh lớn nhất trong ΔDAM
=>DM>DA
mà DA=2DH
nên DM>2DH
c: Xét ΔADF có
H là trung điểm của AD
HE//DF
DO đó: E là trung điểm của AF
Xét ΔADF có
FH,DE là các đường trung tuyến
FH cắt DE tại K
DO đó: K là trọng tâm của ΔADF
=>KD=2KE