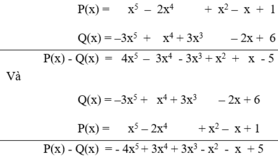Question

[Nguyễn Nhật Long]

a) Tìm tổng P(x)+Q(x)P(x) + Q(x)

Ta có các đa thức:

• P(x)=x4−5x3+4x−5P(x) = x^4 - 5x^3 + 4x - 5
• Q(x)=−x4+3x2+2x+1Q(x) = -x^4 + 3x^2 + 2x + 1

Để tìm tổng P(x)+Q(x)P(x) + Q(x), ta cộng các hệ số của các bậc tương ứng.

P(x)+Q(x)=(x4−5x3+4x−5)+(−x4+3x2+2x+1)P(x) + Q(x) = (x^4 - 5x^3 + 4x - 5) + (-x^4 + 3x^2 + 2x + 1)

Bây giờ, cộng các hạng tử của cùng bậc:

• Bậc 4: x4+(−x4)=0x^4 + (-x^4) = 0
• Bậc 3: −5x3+0=−5x3-5x^3 + 0 = -5x^3
• Bậc 2: 0+3x2=3x20 + 3x^2 = 3x^2
• Bậc 1: 4x+2x=6x4x + 2x = 6x
• Hạng tử tự do: −5+1=−4-5 + 1 = -4

Vậy:

P(x)+Q(x)=−5x3+3x2+6x−4P(x) + Q(x) = -5x^3 + 3x^2 + 6x - 4

b) Tìm đa thức R(x)R(x) sao cho P(x)=R(x)+Q(x)P(x) = R(x) + Q(x)

Để tìm R(x)R(x), ta sử dụng công thức:

P(x)=R(x)+Q(x)P(x) = R(x) + Q(x)

Hay:

R(x)=P(x)−Q(x)R(x) = P(x) - Q(x)

Thay giá trị của P(x)P(x) và Q(x)Q(x) vào công thức:

R(x)=(x4−5x3+4x−5)−(−x4+3x2+2x+1)R(x) = (x^4 - 5x^3 + 4x - 5) - (-x^4 + 3x^2 + 2x + 1)

Khi trừ đi, ta làm thay đổi dấu các hạng tử của Q(x)Q(x):

R(x)=x4−5x3+4x−5+x4−3x2−2x−1R(x) = x^4 - 5x^3 + 4x - 5 + x^4 - 3x^2 - 2x - 1

Bây giờ, cộng các hạng tử của cùng bậc:

• Bậc 4: x4+x4=2x4x^4 + x^4 = 2x^4
• Bậc 3: −5x3+0=−5x3-5x^3 + 0 = -5x^3
• Bậc 2: 0−3x2=−3x20 - 3x^2 = -3x^2
• Bậc 1: 4x−2x=2x4x - 2x = 2x
• Hạng tử tự do: −5−1=−6-5 - 1 = -6

Vậy:

R(x)=2x4−5x3−3x2+2x−6R(x) = 2x^4 - 5x^3 - 3x^2 + 2x - 6

Kết quả:

a) Tổng P(x)+Q(x)=−5x3+3x2+6x−4P(x) + Q(x) = -5x^3 + 3x^2 + 6x - 4

b) Đa thức R(x)=2x4−5x3−3x2+2x−6R(x) = 2x^4 - 5x^3 - 3x^2 + 2x - 6