cho tam giác đều MNP có cạnh=10cm. xác định tâm và bán kính của đtròn ngoại tiếp tam giác MNP
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MT
3 tháng 4 2017
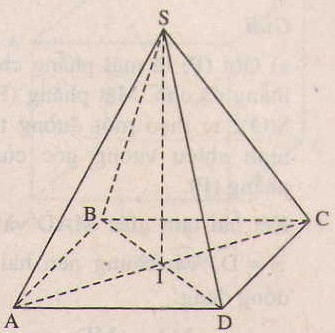
Gọi I = AC ∩ BD. Ta thấy AC = a√2 = BD,
SA = SC = a, nên SA2 + SC2 = AC2. Vậy điểm S nhìn AC dưới một góc vuông. Các điểm B và D cũng nhìn AC dưới một góc vuông.
Vậy mặt cầu ngoại tiếp hình chóp là mặt cầu đường kính AC. Tâm của cầu là điểm I và bán kính R =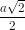 
. Ta thấy rằng điểm I cũng là chân đường cao hạ từ đỉnh S xuống đáy.
23 tháng 8 2021
Tâm là giao điểm của ba đường trung tuyến
Bán kính là bằng 2/3 của độ dài đường trung tuyến
KV
1 tháng 11 2023
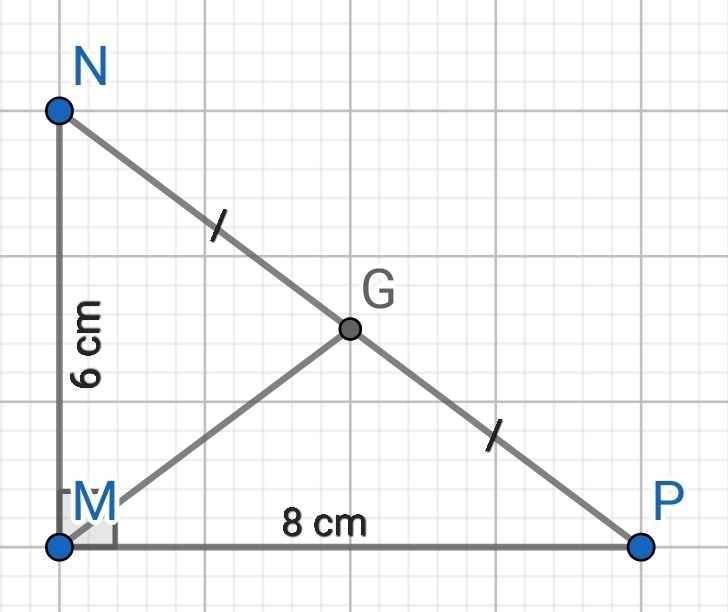
Ta có:
∆MNP vuông tại M
⇒ NP² = MP² + MN² (Pytago)
= 8² + 6² = 100
⇒ NP = 10 (cm)
Gọi G là trung điểm của NP
⇒ MG là đường trung tuyến ứng với cạnh huyền NP của ∆MNP
⇒ MG = NG = PG = NP : 2 = 5 (cm)
⇒ M, N, P cùng thuộc đường tròn tâm G, bán kính MG = 5 cm
9 tháng 11 2023
Stshdtgfdrsgettgstgefdfe📱📱📱📱📱📱💻📱📱📱📱📱📱📱📱💻💻💻💻💻💻📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱🖍️🖍️📱📱📱📱📱📱📱📱📱📱💻📱💻📱💻📱💻📱💻📱💻📱💻📱💻📱💻📱📱💻💻📱💻📱💻📱💻📱📱💻💻📱📱💻📱💻📱💻📱💻📱📱💻📱📱📱📱📱📱📱💻📱💻📱📱💻📱📱📱💻📱💻📱📱📱📱📱📱💻💻💻💻📱📱📱📱
1 tháng 9 2021
Xét tứ giác AEGD có
\(\widehat{AEG}+\widehat{ADG}=180^0\)
Do đó: AEGD là tứ giác nội tiếp
hay A,E,G,D cùng thuộc 1 đường tròn
14 tháng 10 2021
Gọi O là trung điểm BC
Ta có: Tam giác ABC vuông tại A nên đường tròn ngoại tiếp tam giác ABC có cạnh huyền BC là đường kính và O là tâm đường tròn
=> Bán kính là OA,OB,OC
19 tháng 8 2021
a: Xét tứ giác BEDC có
\(\widehat{BEC}=\widehat{BDC}=90^0\)
Do đó: BEDC là tứ giác nội tiếp
Tâm là trung điểm của BC
Bán kính là \(\dfrac{BC}{2}=\dfrac{a}{2}\)
15 tháng 11 2023
a: Xét tứ giác BEDC có
\(\widehat{BEC}=\widehat{BDC}=90^0\)
nên BEDC là tứ giác nội tiếp
=>B,E,D,C cùng thuộc 1 đường tròn
b: Vì \(\widehat{BEC}=\widehat{BDC}=90^0\)
nên B,E,D,C cùng thuộc đường tròn đường kính BC
tâm là trung điểm I của BC
bán kính là BC/2
c: Xét ΔABC có
BD,CE là đường cao
BD cắt CE tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC(1)
ΔABC cân tại A
mà AI là đường trung tuyến
nên AI\(\perp\)BC(2)
Từ (1),(2) suy ra A,H,I thẳng hàng
ΔABC đều
mà BD,CE là các đường cao
nên BD,CE là các đường trung tuyến
=>D,E lần lượt là trung điểm của AC,AB
Xét ΔABC có
BD,CE là các đường trung tuyến
BD cắt CE tại H
Do đó; H là trọng tâm của ΔABC
mà I là trung điểm của BC
nên \(AH=\dfrac{2}{3}AI\) và \(IH=\dfrac{1}{3}IA\)
ΔAIB vuông tại I
=>\(AB^2=AI^2+IB^2\)
=>\(AI^2=2^2-1^2=3\)
=>\(AI=\sqrt{3}\left(cm\right)\)
\(HI=\dfrac{1}{3}HA=\dfrac{1}{3}\sqrt{3}< \dfrac{1}{3}\cdot3=IB=R\)
=>H nằm trong (I)
\(IA=\sqrt{3}>1=IB=R\)
=>A nằm ngoài (I)
Gọi A,B lần lượt là trung điểm của MP,MN. Gọi O là giao điểm của NA và PB
Ta có: \(MB=BN=\dfrac{MN}{2}\)
\(MA=AP=\dfrac{MP}{2}\)
mà MN=MP
nên MB=BN=MA=AP
Xét ΔBNP và ΔAPN có
BN=AP
\(\widehat{BNP}=\widehat{APN}\)
PN chung
Do đó: ΔBNP=ΔAPN
=>\(\widehat{BPN}=\widehat{ANP}\)
=>\(\widehat{ONP}=\widehat{OPN}\)
=>ON=OP
ΔMNP đều
mà PB là đường trung tuyến
nên PB\(\perp\)MN tại B
=>OB\(\perp\)MN tại B
Xét ΔOMN có
OB là đường cao
OB là đường trung tuyến
Do đó: ΔOMN cân tại O
=>OM=ON
mà ON=OP
nên OM=ON=OP
=>O là tâm đường tròn ngoại tiếp ΔMNP
Xét ΔMNP đều có PB là đường trung tuyến
nên \(PB=MN\cdot\dfrac{\sqrt{3}}{2}=5\sqrt{3}\left(cm\right)\)
Xét ΔMNP có
PB,NA là các đường trung tuyến
PB cắt NA tại O
Do đó: O là trọng tâm của ΔMNP
=>\(OP=\dfrac{2}{3}\cdot PB=\dfrac{2}{3}\cdot5\sqrt{3}=\dfrac{10\sqrt{3}}{3}\left(cm\right)\)
=>Bán kính là \(\dfrac{10\sqrt{3}}{3}\left(cm\right)\)