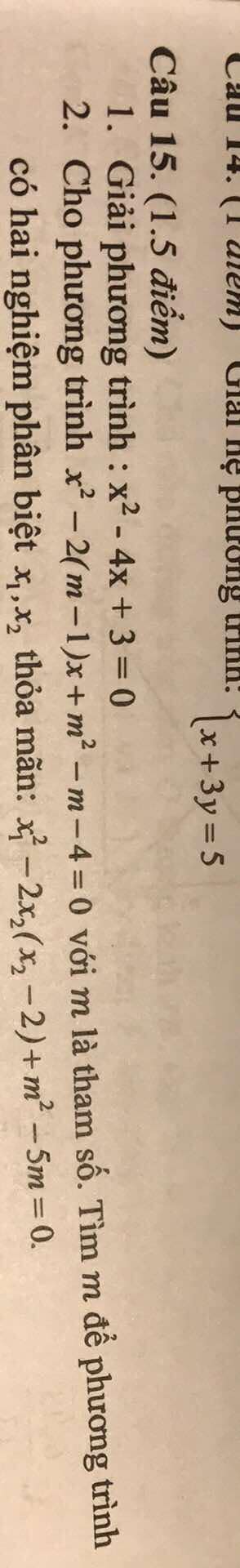 giải giúp tôi phần 2. với
giải giúp tôi phần 2. với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(x-3\right)^3+\left(x+3\right)^3=0\)
\(\Leftrightarrow x^3-9x^2+27x-27+x^3+9x^2+27x+27=0\)\(\Leftrightarrow2x^3+54x^2=0\)
\(\Leftrightarrow x^2\left(2x+54\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\2x+54=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=-27\end{matrix}\right.\)
\(b,\left(x+1\right)^3-\left(x-1\right)^3=0\)
\(\Leftrightarrow x^3+3x^2+3x+1-x^3+3x^2-3x+1=0\)\(\Leftrightarrow6x^2+2=0\)
\(\Leftrightarrow6x^2=-2\)
\(\Leftrightarrow x^2=-3\) ( vô lí)
Vậy pt vô nghiệm
\(c,x^2-4x+3=0\)
\(\Leftrightarrow x^2-3x-x+3=0\)
\(\Leftrightarrow x\left(x-3\right)-\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-3=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)
\(d,4x^2+4x+1=0\)
\(\Leftrightarrow\left(2x+1\right)^2=0\)
\(\Rightarrow2x+1=0\)
\(\Leftrightarrow2x=-1\Rightarrow x=-\dfrac{1}{2}\)
\(e,\left(x+2\right)^2-\left(x+3\right)^2=0\)
\(\Leftrightarrow\left(x+2-x-3\right)\left(x+2+x+3\right)=0\)
\(\Leftrightarrow-\left(2x+5\right)=0\)
\(\Leftrightarrow-2x-5=0\)
\(\Leftrightarrow-2x=5\Rightarrow x=-\dfrac{5}{2}\)
Học tốt nha you <3

\(\left(x-3\right)^3+\left(x+3\right)^3=0\)
\(\Leftrightarrow x^3-9x^2+27x-27+x^3+9x^2+27x+27=0\)\(\Leftrightarrow2x^3+54x^2=0\)
\(\Leftrightarrow x^2\left(2x+54\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\2x+54=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=-27\end{matrix}\right.\)
\(b,\left(x+1\right)^3-\left(x-1\right)^3=0\)
\(\Leftrightarrow x^3+3x^2+3x+1-x^3+3x^2-3x+1=0\)\(\Leftrightarrow6x^2+2=0\)
\(\Leftrightarrow6x^2=-2\)
\(\Leftrightarrow x^2=-3\) ( vô lí)
Vậy pt vô nghiệm
\(c,x^2-4x+3=0\)
\(\Leftrightarrow x^2-3x-x+3=0\)
\(\Leftrightarrow x\left(x-3\right)-\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-3=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)
\(d,4x^2+4x+1=0\)
\(\Leftrightarrow\left(2x+1\right)^2=0\)
\(\Rightarrow2x+1=0\)
\(\Leftrightarrow2x=-1\Rightarrow x=-\dfrac{1}{2}\)
\(e,\left(x+2\right)^2-\left(x+3\right)^2=0\)
\(\Leftrightarrow\left(x+2-x-3\right)\left(x+2+x+3\right)=0\)
\(\Leftrightarrow-\left(2x+5\right)=0\)
\(\Leftrightarrow-2x-5=0\)
\(\Leftrightarrow-2x=5\Rightarrow x=-\dfrac{5}{2}\)
Học tốt nha you <3

\(\left(x-3\right)^3+\left(x+3\right)^3=0\)
\(\Leftrightarrow x^3-9x^2+27x-27+x^3+9x^2+27x+27=0\)\(\Leftrightarrow2x^3+54x^2=0\)
\(\Leftrightarrow x^2\left(2x+54\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\2x+54=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=-27\end{matrix}\right.\)
\(b,\left(x+1\right)^3-\left(x-1\right)^3=0\)
\(\Leftrightarrow x^3+3x^2+3x+1-x^3+3x^2-3x+1=0\)\(\Leftrightarrow6x^2+2=0\)
\(\Leftrightarrow6x^2=-2\)
\(\Leftrightarrow x^2=-3\) ( vô lí)
Vậy pt vô nghiệm
\(c,x^2-4x+3=0\)
\(\Leftrightarrow x^2-3x-x+3=0\)
\(\Leftrightarrow x\left(x-3\right)-\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-3=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)
\(d,4x^2+4x+1=0\)
\(\Leftrightarrow\left(2x+1\right)^2=0\)
\(\Rightarrow2x+1=0\)
\(\Leftrightarrow2x=-1\Rightarrow x=-\dfrac{1}{2}\)
\(e,\left(x+2\right)^2-\left(x+3\right)^2=0\)
\(\Leftrightarrow\left(x+2-x-3\right)\left(x+2+x+3\right)=0\)
\(\Leftrightarrow-\left(2x+5\right)=0\)
\(\Leftrightarrow-2x-5=0\)
\(\Leftrightarrow-2x=5\Rightarrow x=-\dfrac{5}{2}\)
Học tốt nha you <3

a: \(x^3-4x^2-x+4=0\)
=>\(\left(x^3-4x^2\right)-\left(x-4\right)=0\)
=>\(x^2\left(x-4\right)-\left(x-4\right)=0\)
=>\(\left(x-4\right)\left(x^2-1\right)=0\)
=>\(\left[{}\begin{matrix}x-4=0\\x^2-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x^2=1\end{matrix}\right.\Leftrightarrow x\in\left\{2;1;-1\right\}\)
b: Sửa đề: \(x^3+3x^2+3x+1=0\)
=>\(x^3+3\cdot x^2\cdot1+3\cdot x\cdot1^2+1^3=0\)
=>\(\left(x+1\right)^3=0\)
=>x+1=0
=>x=-1
c: \(x^3+3x^2-4x-12=0\)
=>\(\left(x^3+3x^2\right)-\left(4x+12\right)=0\)
=>\(x^2\cdot\left(x+3\right)-4\left(x+3\right)=0\)
=>\(\left(x+3\right)\left(x^2-4\right)=0\)
=>\(\left(x+3\right)\left(x-2\right)\left(x+2\right)=0\)
=>\(\left[{}\begin{matrix}x+3=0\\x-2=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=2\\x=-2\end{matrix}\right.\)
d: \(\left(x-2\right)^2-4x+8=0\)
=>\(\left(x-2\right)^2-\left(4x-8\right)=0\)
=>\(\left(x-2\right)^2-4\left(x-2\right)=0\)
=>\(\left(x-2\right)\left(x-2-4\right)=0\)
=>(x-2)(x-6)=0
=>\(\left[{}\begin{matrix}x-2=0\\x-6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=6\end{matrix}\right.\)

a) Ta có: \(x^2-9x+20=0\)
\(\Leftrightarrow x^2-5x-4x+20=0\)
\(\Leftrightarrow x\left(x-5\right)-4\left(x-5\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-5=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=4\end{matrix}\right.\)
Vậy: x∈{4;5}
b) Ta có: \(x^3-4x^2+5x=0\)
\(\Leftrightarrow x\left(x^2-4x+5\right)=0\)(1)
Ta có: \(x^2-4x+5\)
\(=x^2-4x+4+1=\left(x-2\right)^2+1\)
Ta có: \(\left(x-2\right)^2\ge0\forall x\)
\(\Rightarrow\left(x-2\right)^2+1\ge1>0\forall x\)
hay \(x^2-4x+5>0\forall x\)(2)
Từ (1) và (2) suy ra x=0
Vậy: x=0
c) Sửa đề: \(x^2-2x-15=0\)
Ta có: \(x^2-2x-15=0\)
\(\Leftrightarrow x^2+3x-5x-15=0\)
\(\Leftrightarrow x\left(x+3\right)-5\left(x+3\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left(x-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=5\end{matrix}\right.\)
Vậy: x∈{-3;5}
d) Ta có: \(\left(x^2-1\right)^2=4x+1\)
\(\Leftrightarrow x^4-2x^2+1-4x-1=0\)
\(\Leftrightarrow x^4-2x^2-4x=0\)
\(\Leftrightarrow x\left(x^3-2x-4\right)=0\)
\(\Leftrightarrow x\left(x^3+2x^2+2x-2x^2-4x-4\right)=0\)
\(\Leftrightarrow x\cdot\left[x\left(x^2+2x+2\right)-2\left(x^2+2x+2\right)\right]=0\)
\(\Leftrightarrow x\cdot\left(x^2+2x+2\right)\cdot\left(x-2\right)=0\)(3)
Ta có: \(x^2+2x+2\)
\(=x^2+2x+1+1=\left(x+1\right)^2+1\)
Ta có: \(\left(x+1\right)^2\ge0\forall x\)
\(\Rightarrow\left(x+1\right)^2+1\ge1>0\forall x\)
hay \(x^2+2x+2>0\forall x\)(4)
Từ (3) và (4) suy ra
\(\left[{}\begin{matrix}x=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
Vậy: x∈{0;2}

\(4x^2+4x-3=0\)
\(\left[\left(2x\right)^2+2.2x.1+1\right]-4=0\)
\(\left(2x+1\right)^2-2^2=0\)
\(\left(2x+1-2\right).\left(2x+1+2\right)=0\)
\(\left(2x-1\right).\left(2x+3\right)=0\)
\(\Rightarrow\orbr{\begin{cases}2x-1=0\\2x+3=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{1}{2}\\x=-\frac{3}{2}\end{cases}}}\)
Vậy \(\orbr{\begin{cases}x=\frac{1}{2}\\x=-\frac{3}{2}\end{cases}}\)
\(x^4-3x^3-x+3=0\)
\(x^3.\left(x-3\right)-\left(x-3\right)=0\)
\(\left(x-3\right).\left(x^3-1\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-3=0\\x^3-1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=3\\x=1\end{cases}}}\)
Vậy \(\orbr{\begin{cases}x=3\\x=1\end{cases}}\)
\(x^2.\left(x-1\right)-4x^2+8x-4=0\)
\(x^2.\left(x-1\right)-\left[\left(2x\right)^2-2.2x.2+2^2\right]=0\)
\(x^2.\left(x-1\right)-\left(2x-2\right)^2=0\)
\(x^2.\left(x-1\right)-4.\left(x-1\right)^2=0\)
\(\left(x-1\right).\left[x^2-4.\left(x-1\right)\right]=0\)
\(\left(x-1\right).\left[x^2-2.x.2+2^2\right]=0\)
\(\left(x-1\right).\left(x-2\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-1=0\\x-2=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=1\\x=2\end{cases}}}\)
Vậy \(\begin{cases}x=1\\x=2\end{cases}\)
Tham khảo nhé~


a) \(x^3\)\(-\)\(\frac{1}{4}x\)\(=\)\(0\)
\(x\left(x^2-\frac{1}{4}\right)=0\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}x=0\\x^2-\frac{1}{4}=0\end{cases}}\)\(\Leftrightarrow\)\(\orbr{\begin{cases}x=0\\x^2=0,5^2\end{cases}}\)\(\Leftrightarrow\)\(\orbr{\begin{cases}x=0\\x=+-0,5\end{cases}}\)
Vậy .............................
b) \(\left(2x-1\right)^2\)\(-\)\(\left(x+3\right)^2\)\(=\)\(0\)
\(\left(2x-1+x+3\right)\left(2x-1-x-3\right)=0\)
\(\left(3x+2\right)\left(x-4\right)=0\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}3x+2=0\\x-4=0\end{cases}}\)\(\Leftrightarrow\)\(\orbr{\begin{cases}3x=-2\\x=4\end{cases}}\)\(\orbr{\begin{cases}x=\frac{-2}{3}\\x=4\end{cases}}\)
Vậy ................................
c) \(x^2\)\(\left(x-3\right)\)\(+\)\(12\)\(-\)\(4x\)\(=\)\(0\)
\(x^2\)\(\left(x-3\right)\)\(-\)\(4\)\(\left(x-3\right)\)\(=\)\(0\)
\(\left(x^2-4\right)\left(x-3\right)\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}x^2\\x-3=0\end{cases}-4=0}\)\(\Leftrightarrow\)\(\orbr{\begin{cases}x^2\\x=3\end{cases}=2^2}\)\(\Leftrightarrow\)\(\orbr{\begin{cases}x=+-2\\x=3\end{cases}}\)
a)\(x^3-\frac{1}{4}x=0\)
\(\Leftrightarrow x\left(x^2-\frac{1}{4}\right)=0\)
\(\Leftrightarrow x\left(x-\frac{1}{2}\right)\left(x+\frac{1}{2}\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}x=0\\x-\frac{1}{2}=0\\x+\frac{1}{2}=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=0\\x=\frac{1}{2}\\x=-\frac{1}{2}\end{cases}}}\)

a) \(x^2-4x=0\)
\(x\left(x-4\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x=0\\x-4=0\end{cases}\Rightarrow\orbr{\begin{cases}x=0\\x=4\end{cases}}}\)
b) \(4x^2-9=0\)
\(\left(2x\right)^2-3^2=0\)
\(\left(2x+3\right)\left(2x-3\right)=0\)
\(\Rightarrow\orbr{\begin{cases}2x+3=0\\2x-3=0\end{cases}\Rightarrow\orbr{\begin{cases}x=\frac{-3}{2}\\x=\frac{3}{2}\end{cases}}}\)
c) \(2x\left(x-3\right)+5\left(x-3\right)=0\)
\(\left(x-3\right)\left(2x+5\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-3=0\\2x+5=0\end{cases}\Rightarrow\orbr{\begin{cases}x=3\\x=\frac{-5}{2}\end{cases}}}\)
d) \(x\left(2x+9\right)-4x-18=0\)
\(x\left(2x+9\right)-2\left(2x+9\right)=0\)
\(\left(2x+9\right)\left(x-2\right)=0\)
\(\Rightarrow\orbr{\begin{cases}2x+9=0\\x-2=0\end{cases}\Rightarrow\orbr{\begin{cases}x=\frac{-9}{2}\\x=2\end{cases}}}\)
e) \(\left(2x-1\right)^2-\left(x+2\right)^2=0\)
\(\left(2x-1-x-2\right)\left(2x-1+x+2\right)=0\)
\(\left(x-3\right)\left(3x+1\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-3=0\\3x+1=0\end{cases}\Rightarrow\orbr{\begin{cases}x=3\\x=\frac{-1}{3}\end{cases}}}\)
\(x^2-4x=0\)
\(x.\left(x-4\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\x-4=0\Leftrightarrow x=4\end{cases}}\)
\(4x^2-9=0\)
\(2^2x^2-9=0\)
\(\left(2x\right)^2-9=0\)
\(\left(2x\right)^2-3^2=0\)
\(\Rightarrow\orbr{\begin{cases}\left(2x\right)^2=\left(-3\right)^2\\\left(2x\right)^2=3^2\end{cases}\Rightarrow\orbr{\begin{cases}2x=-3\\2x=3\end{cases}\Rightarrow\orbr{\begin{cases}x=\frac{-3}{2}\\x=\frac{3}{2}\end{cases}}}}\)
\(2x\left(x-3\right)+5\left(x-3\right)=0\)
\(\left(x-3\right)\cdot\left(2x+5\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}\left(x-3\right)=0\\2x+5=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=0+3\\2x=-5\end{cases}\Leftrightarrow\orbr{\begin{cases}x=3\\x=\frac{-5}{2}\end{cases}}}\)
\(x\left(2x+9\right)-4x-18=0\)
\(x\left(2x+9\right)-\left(4x+18\right)=0\)
\(x\left(2x+9\right)-\left(2\cdot2x+2\cdot9\right)=0\)
\(x\left(2x+9\right)-2.\left(2x+9\right)=0\)
\(\left(2x+9\right)\left(x-2\right)=0\Leftrightarrow\orbr{\begin{cases}2x+9=0\\x-2=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}2x=-9\\x=0+2\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{-9}{2}\\x=2\end{cases}}}\)
\(\left(2x-1\right)^2-\left(x+2\right)^2=0\)
\(\Rightarrow\left(2x-1\right)^2=\left(x+2\right)^2\)
\(\Rightarrow\orbr{\begin{cases}2x-1=x+2\\2x-1=-x+2\end{cases}\Rightarrow\orbr{\begin{cases}2x=3+x\\2x=-x+3\end{cases}\Rightarrow\orbr{\begin{cases}2x-x=3\\2x+x=3\end{cases}\Rightarrow\orbr{\begin{cases}x=3\\x=1\end{cases}}}}}\)
\(\)
Câu 1:
x2−4x+3=0x^2 - 4x + 3 = 0x2−4x+3=0
Phương trình này là phương trình bậc hai có dạng chuẩn ax2+bx+c=0ax^2 + bx + c = 0ax2+bx+c=0 với:
Tính biệt số Δ\DeltaΔ:
Δ=b2−4ac=(−4)2−4(1)(3)=16−12=4.\Delta = b^2 - 4ac = (-4)^2 - 4(1)(3) = 16 - 12 = 4.Δ=b2−4ac=(−4)2−4(1)(3)=16−12=4.
Vì Δ>0\Delta > 0Δ>0, phương trình có hai nghiệm phân biệt:
x=−b±Δ2a=4±22.x = \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{4 \pm 2}{2}.x=2a−b±Δ=24±2.
Suy ra hai nghiệm:
x1=4−22=1,x2=4+22=3.x_1 = \frac{4 - 2}{2} = 1, \quad x_2 = \frac{4 + 2}{2} = 3.x1=24−2=1,x2=24+2=3.
Vậy nghiệm của phương trình là x=1x = 1x=1 hoặc x=3x = 3x=3.
Câu 2
Phương trình:
x2−2(m−1)x+m2−m−4=0x^2 - 2(m-1)x + m^2 - m - 4 = 0x2−2(m−1)x+m2−m−4=0
Có hai nghiệm phân biệt khi:
Δ′=(m−1)2−(m2−m−4)>0.\Delta' = (m-1)^2 - (m^2 - m - 4) > 0.Δ′=(m−1)2−(m2−m−4)>0.
Tính toán:
m2−2m+1−m2+m+4>0.m^2 - 2m + 1 - m^2 + m + 4 > 0.m2−2m+1−m2+m+4>0. −m+5>0.- m + 5 > 0.−m+5>0. m<5.m < 5.m<5.
Ta có điều kiện:
x12−2x2(x2−2)+m2−5m=0.x_1^2 - 2x_2(x_2 - 2) + m^2 - 5m = 0.x12−2x2(x2−2)+m2−5m=0.
Sử dụng định lý Vi-ét
x1+x2=2(m−1),x_1 + x_2 = 2(m-1),x1+x2=2(m−1), x1x2=m2−m−4.x_1 x_2 = m^2 - m - 4.x1x2=m2−m−4.
Dùng đẳng thức:
x12=(x1+x2)2−2x1x2.x_1^2 = (x_1 + x_2)^2 - 2x_1 x_2.x12=(x1+x2)2−2x1x2.
Thay vào:
(2(m−1))2−2(m2−m−4)−2x2(x2−2)+m2−5m=0.(2(m-1))^2 - 2(m^2 - m - 4) - 2x_2(x_2 - 2) + m^2 - 5m = 0.(2(m−1))2−2(m2−m−4)−2x2(x2−2)+m2−5m=0.
Biến đổi:
4(m−1)2−2(m2−m−4)−2x22+4x2+m2−5m=0.4(m-1)^2 - 2(m^2 - m - 4) - 2x_2^2 + 4x_2 + m^2 - 5m = 0.4(m−1)2−2(m2−m−4)−2x22+4x2+m2−5m=0.
Dùng x22=(x1+x2)2−2x1x2x_2^2 = (x_1 + x_2)^2 - 2x_1x_2x22=(x1+x2)2−2x1x2, thay vào:
4(m−1)2−2(m2−m−4)−2[(2(m−1))2−2(m2−m−4)]+4x2+m2−5m=0.4(m-1)^2 - 2(m^2 - m - 4) - 2[(2(m-1))^2 - 2(m^2 - m - 4)] + 4x_2 + m^2 - 5m = 0.4(m−1)2−2(m2−m−4)−2[(2(m−1))2−2(m2−m−4)]+4x2+m2−5m=0.
Rút gọn:
4(m2−2m+1)−2m2+2m+8−2[4(m2−2m+1)−2m2+2m+8]+4x2+m2−5m=0.4(m^2 - 2m + 1) - 2m^2 + 2m + 8 - 2[4(m^2 - 2m + 1) - 2m^2 + 2m + 8] + 4x_2 + m^2 - 5m = 0.4(m2−2m+1)−2m2+2m+8−2[4(m2−2m+1)−2m2+2m+8]+4x2+m2−5m=0.
Sau khi tiếp tục biến đổi và rút gọn, ta giải phương trình để tìm các giá trị mmm thỏa mãn.
Kết quả cuối cùng là m=3m = 3m=3 (thỏa mãn cả hai điều kiện trên).