K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 2 2022
Áp dụng định lý Pi-ta-go ta có:
\(AB^2+AC^2=BC^2\\ \Rightarrow21^2+28^2=BC^2\\ \Rightarrow BC=\sqrt{21^2+28^2}\\ \Rightarrow BC=35\left(cm\right)\)
13 tháng 2 2022
Áp dụng định lý Pi-ta-go ta có:
\(NO^2+MO^2=MN^2\\ \Rightarrow MO^2=MN^2-NO^2\\ \Rightarrow MO=\sqrt{55^5-44^2}\\ \Rightarrow MO=33\left(cm\right)\)
16 tháng 1 2023
a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH chung
Do đó: ΔAHB=ΔAKC
b: góc ABH+góc EBC=góc ABC
góc ACK+góc ECB=góc ACB
mà góc ABH=góc ACK;góc ABC=góc ACB
nên góc EBC=góc ECB
=>ΔEBC cân tại E
c: AB=AC
EB=EC
=>AE là trung trực của BC
=>AE vuông góc với BC
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
10 tháng 6 2023
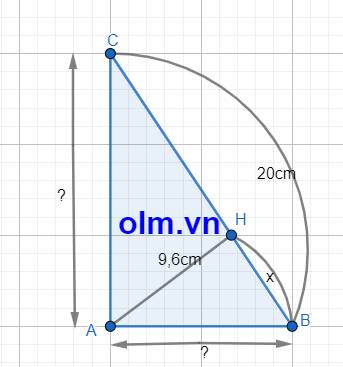
Gọi độ dài đoạn BH là: \(x\) ( cm) ; \(x\) > 0; AC > AB nên \(x\) < CH
Xét tam giác vuông HAB vuông tại H theo pytago ta có:
AB2 = HA2 + HB2 = 9,62 + \(x^2\) = 92,16 + \(x^2\)
Xét tam giác vuông AHC vuông tại H theo pytago ta có:
AC2 = HA2 + HC2 = 9,62 + (\(20-x\))2 = 92,16 + 400 - 40\(x\) + \(x^2\)
AC2 = 492,16 - 40\(x\) + \(x^2\)
Xét tam giác vuông ABC vuông tại A theo pytago ta có:
AC2 + AB2 = BC2
492,16 - 40\(x\) + \(x^2\) + 92,16 + \(x^2\) = 202
(\(x^2\) + \(x^2\)) - 40\(x\) + (492,16 + 92,16) - 400 = 0
2\(x^2\) - 40\(x\) + 584,32 - 400 = 0
2\(x^2\)- 40\(x\) + 184,32 =0
\(x^2\) - 20\(x\) + 92,16 = 0
△' = 102 - 92,16 = 7,84 > 0
\(x\)1 = -(-10) + \(\sqrt{7,84}\) = 12,8 ⇒ CH = 20 - 12,8 = 7,2 < BH (loại )
\(x_2\) = -(-10) - \(\sqrt{7,84}\) = 7,2 ⇒ CH = 20 - 7,2 = 12,8 (thỏa mãn)
Thay \(x_2\) = 7,2 vào biểu thức: AB2 = 92,16 + \(x^2\) = 92,16 + 7,22 = 144
⇒AB = \(\sqrt{144}\) = 12
Thay \(x_2\) = 7,2 vào biểu thức: AC2 = 492,16 - 40\(x\) + \(x^2\)
AC2 = 492,16 - 40\(\times\) 7,2 + 7,22 = 256
AC = \(\sqrt{256}\) = 16
Kết luận AB = 12 cm; AC = 16 cm
10 tháng 5 2022
a: Xét ΔIHM vuông tại H và ΔINM vuông tại N có
IM chung
\(\widehat{HIM}=\widehat{NIM}\)
Do đó: ΔIHM=ΔINM
b: ta có: ΔIHM=ΔINM
nên HM=NM
c: Ta có: HM=MN
mà MN<MK
nên HM<MK
GH
28 tháng 7 2023
Tam giác ABC vuông tại B
=> \(\widehat{B}=90^o\)
Áp dụng định lý tổng 3 góc trong 1 tam giác vào tam giác ABC vuông tại B có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\\ \Rightarrow55^o+90^o+\widehat{C}=180^o\\ \Rightarrow\widehat{C}=180^o-90^o-55^o=35^o\)
Vậy số đo góc C là `35^o`
a: Xét ΔBHA vuông tại H và ΔBAC vuông tại A có
\(\widehat{HBA}\) chung
Do đó: ΔBHA~ΔBAC
=>\(\dfrac{BH}{BA}=\dfrac{BA}{BC}\)
=>\(BA^2=BH\cdot BC\)
Xét ΔCHA vuông tại H và ΔCAB vuông tại A có
\(\widehat{HCA}\) chung
Do đó ΔCHA~ΔCAB
=>\(\dfrac{CH}{CA}=\dfrac{CA}{CB}\)
=>\(CA^2=CH\cdot CB\)
b: ΔCHA~ΔCAB
=>\(\dfrac{CA}{CB}=\dfrac{AH}{AB}\)
=>\(AB\cdot AC=AH\cdot BC\)
c: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{HBA}\right)\)
Do đó: ΔHAB~ΔHCA
=>\(\dfrac{HA}{HC}=\dfrac{HB}{HA}\)
=>\(HA^2=HB\cdot HC\)
d: \(\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{AB^2+AC^2}{\left(AB\cdot AC\right)^2}=\dfrac{BC^2}{\left(BC\cdot AH\right)^2}=\dfrac{1}{AH^2}\)
e: \(AH^2=HB\cdot HC=4\cdot9=36\)
=>\(AH=\sqrt{36}=6\left(cm\right)\)
BC=BH+CH=4+9=13(cm)
ΔABC có AH là đường cao
nên \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot6\cdot13=39\left(cm^2\right)\)
a) Xét hai tam giác vuông: ∆ABC và ∆HBA có:
∠B chung
⇒ ∆ABC ∽ ∆HBA (g-g)
⇒ AB² = BH.BC
Xét hai tam giác vuông: ∆ABC và ∆HAC có:
∠C chung
⇒ ∆ABC ∽ ∆HAC (g-g)
⇒ AC² = CH.BC
b) Do ∆ABC ∽ ∆HBA (cmt)
⇒ AH.BC = AB.AC
c) Do ∆ABC ∽ ∆HBA (cmt)
∆ABC ∽ ∆HAC (cmt)
⇒ ∆HBA ∽ ∆HAC
⇒ AH² = BH.CH
d) Do AH.BC = AB.AC (cmt)
Do ∆ABC vuông tại A (gt)
⇒ BC² = AB² + AC² (Pythagore)
Thế BC² = AB² + AC² vào (1), ta được:
e) Ta có:
BC = BH + CH = 4 + 9 = 13
Lại có:
AH² = BH.CH (cmt)
⇒ AH² = 4.9 = 36
⇒ AH = 6
Diện tích ∆ABC
S = 6 . 13 : 2 = 39 (đvdt)