em không lấy được kết quả bài này ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 4:
PTHH: \(NaBr+AgNO_3\rightarrow NaNO_3+AgBr\downarrow\)
a) Ta có: \(n_{AgBr}=\dfrac{37,6}{188}=0,2\left(mol\right)=n_{NaBr}\)
\(\Rightarrow\%m_{NaBr}=\dfrac{0,2\cdot103}{42,6}\cdot100\%\approx48,37\%\) \(\Rightarrow\%m_{NaF}=51,63\%\)
b) Ta có: \(\Sigma n_{AgNO_3}=\dfrac{850\cdot1,09\cdot10\%}{170}=0,545\left(mol\right)\)
\(\Rightarrow n_{AgNO_3\left(dư\right)}=0,345\left(mol\right)\) \(\Rightarrow m_{AgNO_3\left(dư\right)}=0,345\cdot170=58,65\left(g\right)\)
Theo PTHH: \(m_{NaNO_3}=0,2\cdot85=17\left(g\right)\)
Mặt khác: \(\left\{{}\begin{matrix}m_{NaF}=42,6-0,2\cdot103=22\left(g\right)\\m_{dd}=m_{hh}+m_{ddAgNO_3}-m_{AgBr}=931,5\left(g\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}C\%_{AgNO_3\left(dư\right)}=\dfrac{58,65}{931,5}\cdot100\%\approx6,3\%\\C\%_{NaF}=\dfrac{22}{931,5}\cdot100\%\approx2,36\%\\C\%_{NaNO_3}=\dfrac{17}{931,5}\cdot100\%\approx1,83\%\end{matrix}\right.\)
Em từng nghe là vì chưa biết HCl dư hay hết nên không được dùng ngay số mol của HCl , với cả đề còn dữ kiện 11,2l khí chưa đc khai thác

Câu 50 thì bạn nhóm cặp lại tan1*tan89*tan2*tan88*...*tan45
thì bạn sẽ thấy là tan1*tan89=tan2*tan88=...=tan45=1
=>D
Câu 51 thì bạn nhóm cặp lại \(sin^288^0;sin^22^0\); sin2860 và sin240;...;sin244 độ và sin2 46 độ thì bạn sẽ thấy từng cặp đó có tổng bằng 1
Và có 22 cặp như vậy nên đáp án là C

con số mà Dương cộng với 19,81 là:
2118-19,81=137
kết quả đúng của phép cộng là
137+19,81=156,81
đáp số : 156,81

Bạn nói đúng vì:
Điện trở tương đương của đoạn mạch là :
Rtđ=R1+ R2=30+50=80 (ôm)
Vì R1 mắc nối tiếp với R2 nên :
I1=I2=I=U/Rtđ=24/80=0,3 (A)
HĐT giữa 2 đầu R2 là :
U2=I2.R2= 0,3 . 50 = 15 (V)

Điện xoay chiều thú vị ở chỗ đó, chúng ta có thể dùng biến đổi đại số, dùng giản đồ véc tơ (tạm gọi là véc tơ thường - véc tơ buộc và véc tơ trượt), ngoài ra còn có thể dùng số phức để giải. Tùy từng bài toán và tùy từng kinh nghiệm của mỗi người thì sẽ biết nên làm theo cách nào cho hợp lí. Em hãy cứ làm nhiều bài tập điện xoay chiều thì em sẽ nhận ra điều đó.
Dùng giản đồ véc tơ thường thì hầu như dạng bài tập nào cũng giải được.
Còn véc tơ trượt là một biến thể của véc tơ thường (dựa vào tính chất cộng véc tơ trong toán học), làm cho hình vẽ đỡ rối hơn.
Còn nên dùng theo cách nào thì như mình nói tùy từng bài toán và kinh nghiệm của mỗi người. Kinh nghiệm của mình là những bài toán mà cho mối liên hệ các điện áp chéo nhau (VD: URL, URC,...) thì dùng véc tơ thường, trường hợp còn lại thì dùng véc tơ trượt.

Bài 1:
ĐKXĐ: \(x\ge\dfrac{1}{2}\)
Ta có: \(\sqrt{5x^2}=2x-1\)
\(\Leftrightarrow5x^2=\left(2x-1\right)^2\)
\(\Leftrightarrow5x^2-4x^2+4x-1=0\)
\(\Leftrightarrow x^2+4x-1=0\)
\(\text{Δ}=4^2-4\cdot1\cdot\left(-1\right)=20\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-4-2\sqrt{5}}{2}=-2-\sqrt{5}\left(loại\right)\\x_2=\dfrac{-4+2\sqrt{5}}{2}=-2+\sqrt{5}\left(loại\right)\end{matrix}\right.\)
Bài 1: Bình phương hai vế lên có giải ra được kết quả. Nhưng phải kèm thêm điều kiện $2x-1\geq 0$ do $\sqrt{5x^2}\geq 0$
PT \(\Leftrightarrow \left\{\begin{matrix} 2x-1\geq 0\\ 5x^2=(2x-1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x^2+4x-1=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2)^2-5=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2-\sqrt{5})(x+2+\sqrt{5})=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x=-2\pm \sqrt{5}\end{matrix}\right.\) (vô lý)
Vậy pt vô nghiệm.

Phần bên trên giải thích rồi còn gì
n + n - 1 + n - 2 + n - 3 + .... + 1
Tổng của dãy số hơn kém 1 đơn vị lùi từ n về 1
T = (Số đầu - số cuối) . số số hạng rồi chia 2
tức là \(\dfrac{\left(n-1\right).n}{2}\)

Đây là công thức bạn phải thuộc lòng, còn b là số lớn 0 và khác 1, tùy vào bài tập bạn giải sẽ có số b hợp lý.


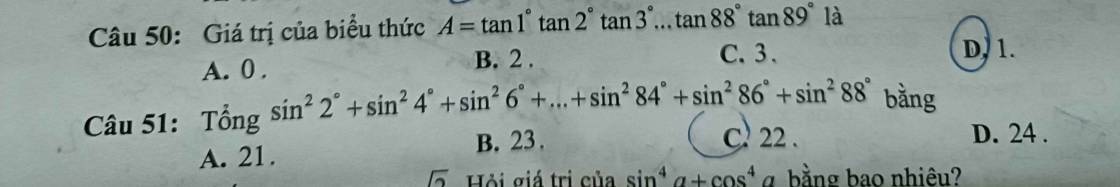
 thầy @phynit câu này hình như nhầm lẫn vì kết quả là 15V thầy ạ. vì em báo lỗi không được nên đăng lên để thầy sữa kịp thời
thầy @phynit câu này hình như nhầm lẫn vì kết quả là 15V thầy ạ. vì em báo lỗi không được nên đăng lên để thầy sữa kịp thời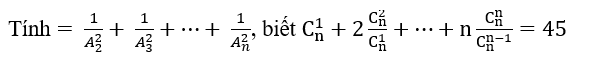
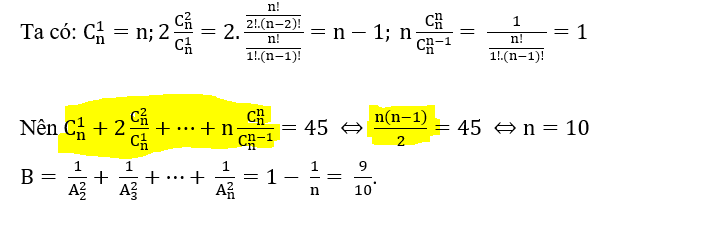
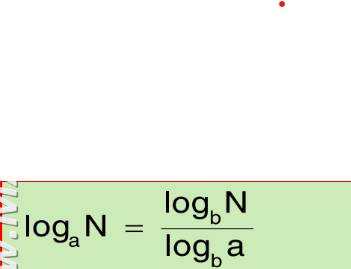
bai nao
bai nao vay e