Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn D.
Phương pháp: Sử dụng các tính chất hàm số đa thức bậc 3.
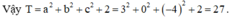
a.
Do (P) đi qua F, thay tọa độ F vào phương trình (P) ta được:
\(a.0^2+b.0+c=5\Rightarrow c=5\)
Do (P) có đỉnh \(I\left(3;-4\right)\)
\(\Rightarrow\left\{{}\begin{matrix}-\dfrac{b}{2a}=3\\a.3^2+b.3+c=-4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}b=-6a\\9a+3b+5=-4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=-6a\\9a+3.\left(-6a\right)=-9\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=-6\end{matrix}\right.\)
hay pt (P) có dạng: \(y=x^2-6x+5\)
b. Em tự giải
Theo đề, ta có: c=4
Theo đề, ta có:
\(\left\{{}\begin{matrix}-\dfrac{b}{2a}=1\\-\dfrac{b^2}{16a}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\4a^2+80a=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-20\\b=40\end{matrix}\right.\)
Đáp án C
Phương pháp giải:
Chọn hệ số a, b, c hoặc đánh giá tích để biện luận số nghiệm của phương trình
Lời giải:
Cách 1. Ta có: 
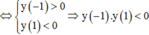
Lại có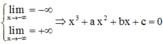 
có 3 nghiệm thuộc khoảng 
Cách 2. Chọn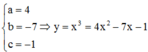 
và đồ thị hàm số cắt trục Ox tại 3 điểm phân biệt
\(y=x^3+ax^2+bx+c\)
\(\rArr y^{\prime}=3x^2+2ax+b\)
Theo đề bài, ta có y(0) = 1 \(\rArr c=1\)
và y(-2) = 0 \(\rArr\left(-2\right)^3+a\left(-2\right)^2+b\left(-2\right)+1=0\)
\(\rArr-8+4a-2b+1=0\)
\(\rArr4a-2b=7\) (1)
Lại có y'(-2) = 0 \(\rArr3\left(-2\right)^2+2a\left(-2\right)+b=0\)
\(\rArr4a-b=12\) (2)
Lấy (2) trừ vế theo vế với (1), ta có \(b=5\) \(\rArr a=\frac{17}{4}\)
\(\rArr a^2+b^2+c^2=\left(\frac{17}{4}\right)^2+5^2+1^2=\frac{705}{16}\) (khoảng 44,1)