Câu 19. Vật dao động điều hòa theo phương trình x = 8cos(4pi*t) , cm. Thời điểm lần đầu tiên vật qua vị trí có li độ bằng -4căn 3 cm theo chiều dương là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Thời điểm đầu tiên vật qua vị trí có li độ x = -12 cm

Tốc độ của vật tại thời điểm t = 2/3 s
![]()
⇒ v ≈ 0,33 m/s

Thời điểm đầu tiên vật đi qua li độ x = -12 cm là
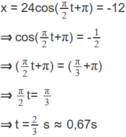
Tốc độ tại thời điểm t = 2/3s là:
v = - ω Asin( π /3 + π ) = 32,6 cm/s ≈ 33 cm/s

`a)A=4 (cm)`
`\omega=2\pi .f=10\pi (rad//s)`
Tại `t=0` thì `x_0 =-4=>\varphi=\pi (rad)`
`=>` Ptr: `x=4cos(10\pi t+\pi)`.
`b)` Ta có: `t=T/4 -T/6=T/12 =1/12 . [2\pi]/[10\pi]=1/60 (s)`
`c)T=[2\pi]/[10\pi]=0,2(s)`
`=>` Trong `2s` vật đi được `t=2/[0,2]=10T`
`=>` Quãng đường đi được trong `2s` là: `s=10.4.A=160(cm)`.

Chọn D.
Từ đồ thị suy ra: T = 0,4s.
Cứ mỗi nửa chu kì, đường x = 2cm cắt đồ thị tại 1 điểm mà t = 1s = 5.0,2 = 5.T/2 nên sẽ cắt đồ thị tai 5 điểm.

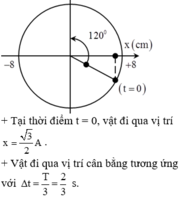
Ta có \(A=8cm;\omega=4\pi rad/s;\varphi_0=0rad\) \(\Rightarrow T=\dfrac{2\pi}{\omega}=0,5\left(s\right)\)
Vật đi qua vị trí có li độ bằng \(-4\sqrt{3}cm\) theo chiều dương thì \(\varphi=\dfrac{4\pi}{3}\)
\(\Rightarrow\Delta\varphi=\dfrac{4\pi}{3}\left(rad\right)\)
\(\Rightarrow\Delta t=\dfrac{\Delta\varphi}{2\pi}.T=\dfrac{\dfrac{4\pi}{3}}{2\pi}.0,5=\dfrac{1}{3}\left(s\right)\)
Vậy thời gian để vật đi qua vị trí có li độ bằng \(-4\sqrt{3}cm\) theo chiều dương là \(\dfrac{1}{3}s\)