 Các thầy cô và các bạn giúp em với ạ !!
Các thầy cô và các bạn giúp em với ạ !!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Số tiền (cả vốn lẫn lãi) bác Minh thu được sau 3 năm là: 100.(1 + 6%)3 = 119,1016 (triệu đồng)

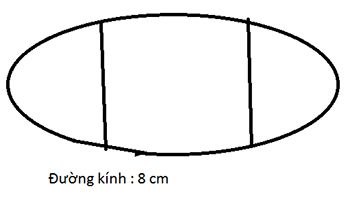
Gọi tứ giác nằm ngang là ABCD.
Hình dựng đứng là ABEMN
Từ điểm M kẻ đường thẳng//AB cắt BE tại G.
Do NM_|_AN tại A
MN//AB; BG//AN
=>BG_|_BE nên tam giác MGE vuông tại G. (1)
=>Tứ giác ABGN là hình chữ nhật=Hình chữ nhật ABCD( vì AB//=CD=14,2 m)
=>AN=AC=5 (m)
Từ (1) =>EG là đường cao của tam giác MGE có cạnh đáy MG.
=>EG=BE-BG=8-5=3 (m)
=>MG=NG-MN=14,2-6,2=8 (m)
Vậy S(MGE)=1/2.EG.MG=1/2.3.8=12 (m2)
=>S(ABCD)+S(ABGN)=2. S(ABCD)
=2.AB.AD=2.5.14,2=142 (m2)
=> Diện tích hình đã cho bằng:
12+142=154 m2
Đ s:
Gọi tứ giác nằm ngang là ABCD.
Hình dựng đứng là ABEMN
Từ điểm M kẻ đường thẳng//AB cắt BE tại G.
Do NM_|_AN tại A
MN//AB; BG//AN
=>BG_|_BE nên tam giác MGE vuông tại G. (1)
=>Tứ giác ABGN là hình chữ nhật=Hình chữ nhật ABCD( vì AB//=CD=14,2 m)
=>AN=AC=5 (m)
Từ (1) =>EG là đường cao của tam giác MGE có cạnh đáy MG.
=>EG=BE-BG=8-5=3 (m)
=>MG=NG-MN=14,2-6,2=8 (m)
Vậy S(MGE)=1/2.EG.MG=1/2.3.8=12 (m2)
=>S(ABCD)+S(ABGN)=2. S(ABCD)
=2.AB.AD=2.5.14,2=142 (m2)
=> Diện tích hình đã cho bằng:
12+142=154 m2


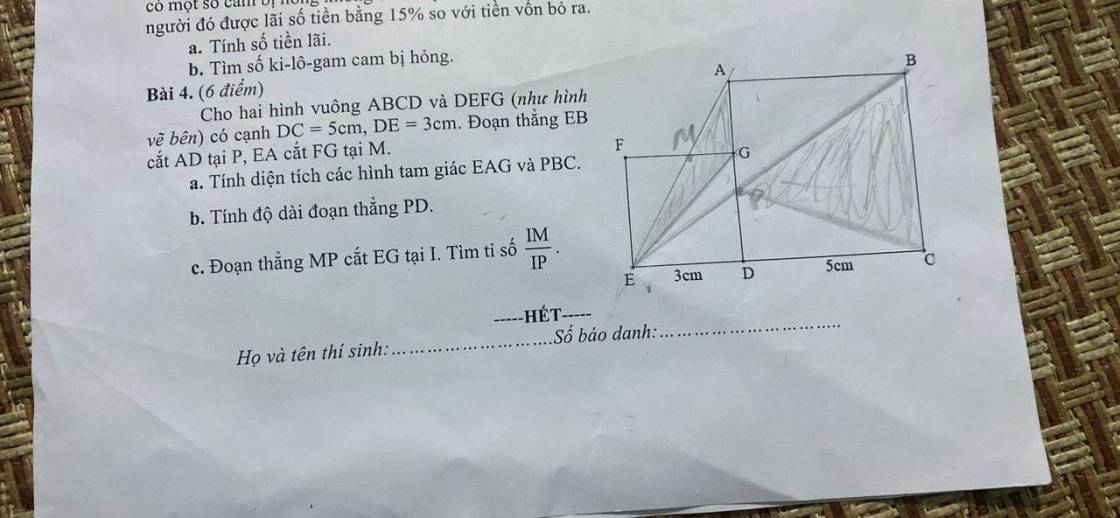
a) \(S_{EAG}=\dfrac{1}{2}\times AG\times ED=\dfrac{1}{2}\times2\times3=3\left(cm^2\right)\)
\(S_{PBC}=\dfrac{1}{2}\times BC\times DC=\dfrac{1}{2}\times5\times5=12,5\left(cm^2\right)\)
b) Ta có:
\(S_{EBC}=\dfrac{1}{2}\times BC\times EC=\dfrac{1}{2}\times5\times8=20\left(cm^2\right)\)
\(S_{PEC}=S_{ECB}-S_{PBC}=20-12,5=7,5\left(cm^2\right)\)
Vậy nên:
\(PD=\dfrac{2\times S_{PEC}}{EC}=\dfrac{2\times7,5}{8}=1,875\left(cm\right)\)
c) Ta thấy:
\(\dfrac{IM}{IP}=\dfrac{S_{MIG}}{S_{IPG}}=\dfrac{S_{MIE}}{S_{IPE}}\) nên \(\dfrac{IM}{IP}=\dfrac{S_{MGE}}{S_{GPE}}=\dfrac{\dfrac{1}{2}\times MG\times3}{\dfrac{1}{2}\times GP\times3}=\dfrac{MG}{GP}\)
Kéo dài AD cắt EF tại K.
Ta có \(S_{AKM}=\dfrac{1}{2}\times3\times2=3\left(cm^2\right)\)
nên \(S_{EKM}=S_{AKE}-S_{AKM}=\dfrac{1}{2}\times3\times5-3=4,5\left(cm^2\right)\)
Vậy \(FM=\dfrac{2\times S_{EKM}}{KE}=1,8\left(cm\right)\)
Thế thì \(MG=3-1,8=1,2\left(cm\right)\)
Lại có \(GP=3-1,875=1,125\left(cm\right)\)
Vậy nên:
\(\dfrac{IM}{IP}=\dfrac{MG}{GP}=\dfrac{1,2}{1,125}=\dfrac{16}{15}\).
Tttt
Ggghghnkhg