B2: Cho bth A=
a. Viết điều kiên xác đinh của bt A
c) tính g trị của biểu thức B tại x=3/5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
T
25 tháng 12 2023
a) ĐKXĐ: \(x\ne\pm1\)
b) \(A=\dfrac{x^3-1}{x^2-1}\cdot\left(\dfrac{1}{x-1}-\dfrac{x+1}{x^2+x+1}\right)\left(dkxd:x\ne\pm1\right)\)
\(=\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{\left(x-1\right)\left(x+1\right)}\cdot\left[\dfrac{x^2+x+1}{\left(x-1\right)\left(x^2+x+1\right)}-\dfrac{\left(x-1\right)\left(x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\right]\)
\(=\dfrac{x^2+x+1}{x+1}\cdot\dfrac{x^2+x+1-\left(x^2-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x^2+x+1-x^2+1}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{x+2}{x^2-1}\)
c) Có: \(\left|x+3\right|=1\Leftrightarrow\left[{}\begin{matrix}x+3=1\\x+3=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=-4\end{matrix}\right.\left(tmdk\right)\)
+) Với \(x=-2\), thay vào \(A\), ta được:
\(A=\dfrac{-2+2}{\left(-2\right)^2-1}=0\)
+) Với \(x=-4\), thay vào \(A\), ta được:
\(A=\dfrac{-4+2}{\left(-4\right)^2-1}=-\dfrac{2}{15}\)
\(\text{#}Toru\)
30 tháng 10 2023
a) ĐKXĐ:
\(x^2-1\ne0\Leftrightarrow x\ne\pm1\)
b) \(A=\dfrac{x^2-2x+1}{x^2-1}\)
\(A=\dfrac{x^2-2\cdot x\cdot1+1^2}{x^2-1^2}\)
\(A=\dfrac{\left(x-1\right)^2}{\left(x+1\right)\left(x-1\right)}\)
\(A=\dfrac{x-1}{x+1}\)
c) Thay x = 3 vào A ta có:
\(A=\dfrac{3-1}{3+1}=\dfrac{2}{4}=\dfrac{1}{2}\)
30 tháng 10 2023
a) ĐKXĐ:
\(9x^2-y^2\ne0\Leftrightarrow\left(3x\right)^2-y^2\ne0\Leftrightarrow\left(3x-y\right)\left(3x+y\right)\ne0\)
\(\Leftrightarrow3x\ne\pm y\)
b) \(B=\dfrac{6x-2y}{9x^2-y^2}\)
\(B=\dfrac{2\cdot3x-2y}{\left(3x\right)^2-y^2}\)
\(B=\dfrac{2\left(3x-y\right)}{\left(3x+y\right)\left(3x-y\right)}\)
\(B=\dfrac{2}{3x+y}\)
Thay x = 1 và \(y=\dfrac{1}{2}\) và B ta có:
\(B=\dfrac{2}{3\cdot1+\dfrac{1}{2}}=\dfrac{2}{3+\dfrac{1}{2}}=\dfrac{2}{\dfrac{7}{2}}=\dfrac{4}{7}\)
22 tháng 11 2021
\(a,ĐK\left(A\right):x\ne-\dfrac{3}{2};ĐK\left(B\right):x\ne-1;x\ne-3\\ b,A=\dfrac{-1+1}{2\left(-1\right)+3}=0\\ B=\dfrac{2\left(-\dfrac{2}{3}\right)+3}{1-\dfrac{2}{3}}+\dfrac{2-\dfrac{2}{3}}{3-\dfrac{2}{3}}=\dfrac{3-\dfrac{4}{3}}{\dfrac{1}{3}}+\dfrac{4}{3}:\dfrac{7}{3}=\dfrac{5}{3}:\dfrac{1}{3}+\dfrac{4}{7}=5+\dfrac{4}{7}=\dfrac{39}{7}\)
TM
26 tháng 1 2022
1. ĐKXĐ: \(x\ne\pm1\)
2. \(A=\left(\dfrac{x+1}{x-1}-\dfrac{x+3}{x+1}\right)\cdot\dfrac{x+1}{2}\)
\(=\dfrac{\left(x+1\right)^2-\left(x-3\right)\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{2}\)
\(=\dfrac{x^2+2x+1-x^2+4x-3}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{2}\)
\(=\dfrac{6x-2}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{2}\)
\(=\dfrac{2\left(x-3\right)\left(x+1\right)}{2\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{x-3}{x-1}\)
3. Tại x = 5, A có giá trị là:
\(\dfrac{5-3}{5-1}=\dfrac{1}{2}\)
4. \(A=\dfrac{x-3}{x-1}\) \(=\dfrac{x-1-3}{x-1}=1-\dfrac{3}{x-1}\)
Để A nguyên => \(3⋮\left(x-1\right)\) hay \(\left(x-1\right)\inƯ\left(3\right)=\left\{1;-1;3;-3\right\}\)
\(\Rightarrow\left\{{}\begin{matrix}x-1=1\\x-1=-1\\x-1=3\\x-1=-3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=2\left(tmđk\right)\\x=0\left(tmđk\right)\\x=4\left(tmđk\right)\\x=-2\left(tmđk\right)\end{matrix}\right.\)
Vậy: A nguyên khi \(x=\left\{2;0;4;-2\right\}\)
18 tháng 12 2023
Bài 1:
a: Sửa đề \(x^3y-2x^2y+xy\)
\(=y\left(x^3-2x^2+x\right)\)
\(=x\cdot y\cdot\left(x^2-2x+1\right)\)
\(=xy\left(x-1\right)^2\)
b: Sửa đề: \(x^2-9-2xy+y^2\)
\(=\left(x^2-2xy+y^2\right)-9\)
\(=\left(x-y\right)^2-9\)
\(=\left(x-y-3\right)\left(x-y+3\right)\)
Bài 2:
a: ĐKXĐ: \(x\notin\left\{3;-3;-1\right\}\)
b: \(A=\left(\dfrac{x}{x+3}-\dfrac{2}{x-3}+\dfrac{x^2-1}{9-x^2}\right):\left(2-\dfrac{x+5}{x+3}\right)\)
\(=\left(\dfrac{x}{x+3}-\dfrac{2}{x-3}-\dfrac{x^2-1}{\left(x-3\right)\left(x+3\right)}\right):\dfrac{2x+6-x-5}{x+3}\)
\(=\dfrac{x\left(x-3\right)-2\left(x+3\right)-x^2+1}{\left(x+3\right)\left(x-3\right)}\cdot\dfrac{x+3}{x+1}\)
\(=\dfrac{x^2-3x-2x-6-x^2+1}{x-3}\cdot\dfrac{1}{x+1}\)
\(=\dfrac{-5x-5}{\left(x-3\right)\left(x+1\right)}=-\dfrac{5\left(x+1\right)}{\left(x-3\right)\left(x+1\right)}=-\dfrac{5}{x-3}\)
c: \(x^2-x-2=0\)
=>\(\left(x-2\right)\left(x+1\right)=0\)
=>\(\left[{}\begin{matrix}x-2=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\left(nhận\right)\\x=-1\left(loại\right)\end{matrix}\right.\)
Thay x=2 vào A, ta được:
\(A=\dfrac{-5}{2-3}=\dfrac{-5}{-1}=5\)
TM
20 tháng 1 2022
a. ĐKXĐ: \(x\ne\pm1\)
b. \(A=\left(x^2-1\right)\left(\dfrac{1}{x-1}-\dfrac{1}{x+1}-1\right)\)
\(=\left(x-1\right)\left(x+1\right)\left[\dfrac{x+1}{\left(x-1\right)\left(x+1\right)}-\dfrac{x-1}{\left(x-1\right)\left(x+1\right)}-\dfrac{\left(x-1\right)\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\right]\)
\(=\left(x-1\right)\left(x+1\right)\left[\dfrac{x+1-x+1-\left(x-1\right)\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\right]\)
\(=\left(x-1\right)\left(x+1\right)\left[\dfrac{-x^2+3}{\left(x-1\right)\left(x+1\right)}\right]\)
\(=\dfrac{\left(x-1\right)\left(x+1\right)\left(-x^2+3\right)}{\left(x-1\right)\left(x+1\right)}\)
\(=-x^2+3\)
c. Thay x = 3 vào A ta được:
\(-\left(3\right)^2+3=-6\)
Vậy: Giá trị của A tại x = 3 là -6
20 tháng 1 2022
a) ĐKXĐ: \(x\ne1;x\ne-1.\)
b) \(A=\left(x^2-1\right).\left(\dfrac{1}{x-1}-\dfrac{1}{x+1}-1\right).\)
\(=\left(x^2-1\right).\dfrac{x+1-x+1-x^2+1}{x^2-1}=-x^2+3.\)
c) Thay x = 3 (TMĐK) vào A: \(-3^2+3=-6.\)
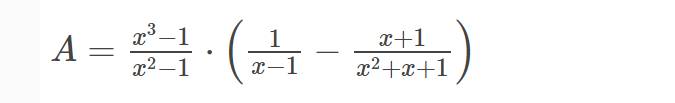
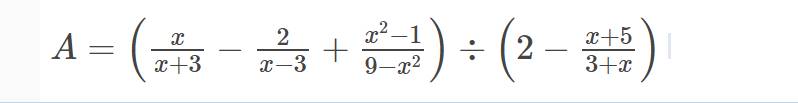
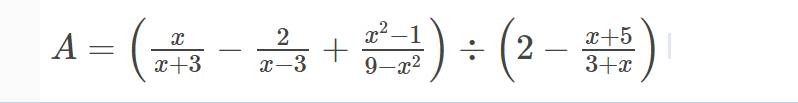
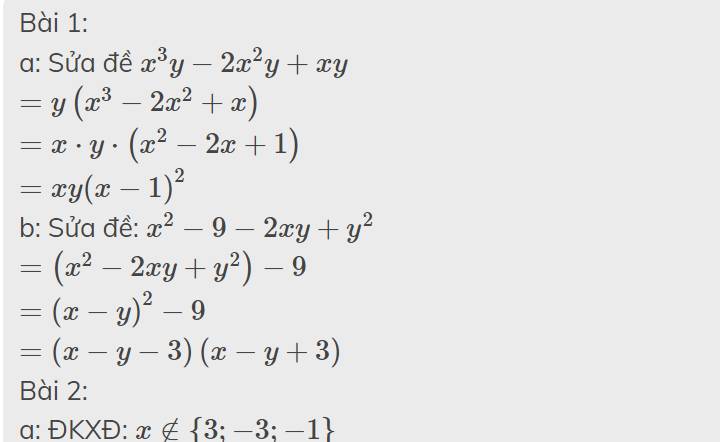
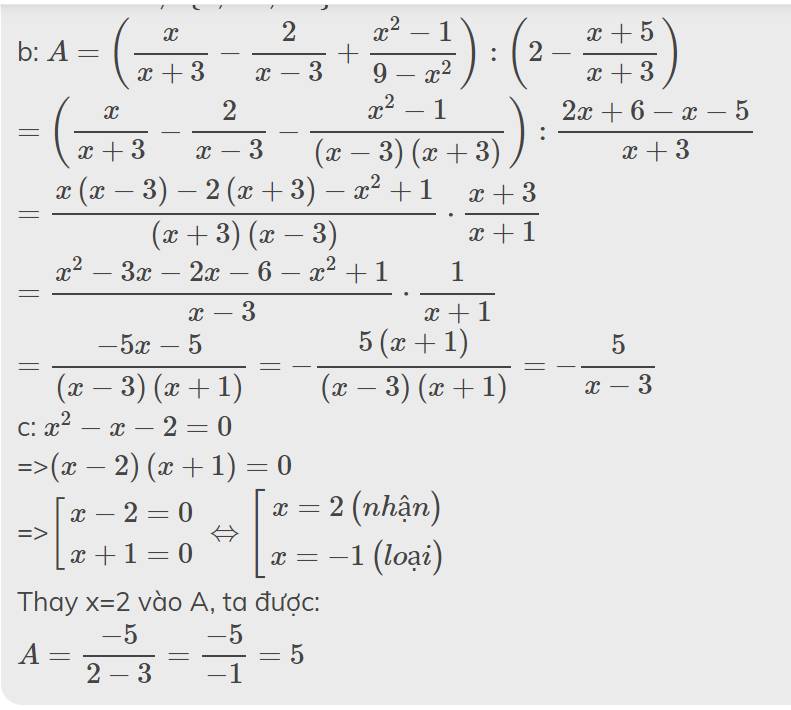
a: ĐKXĐ: \(x\notin\left\{\dfrac{3}{2};\dfrac{1}{5};-\dfrac{1}{5}\right\}\)
b: Sửa đề: của biểu thức A tại x=3/5
\(A=\dfrac{5x+1}{2x-3}\cdot\dfrac{x+2}{25x^2-1}:\dfrac{2x-3}{5x+1}\)
\(=\dfrac{5x+1}{2x-3}\cdot\dfrac{x+2}{\left(5x-1\right)\left(5x+1\right)}\cdot\dfrac{5x+1}{2x-3}\)
\(=\dfrac{\left(x+2\right)}{\left(2x-3\right)^2}\)
Khi x=3/5 thì \(A=\dfrac{\left(\dfrac{3}{5}+2\right)}{\left(2\cdot\dfrac{3}{5}-3\right)^2}=\dfrac{13}{5}:\left(\dfrac{6}{5}-3\right)^2\)
\(=\dfrac{13}{5}:\left(-\dfrac{9}{5}\right)^2\)
\(=\dfrac{13}{5}:\dfrac{81}{25}=\dfrac{13}{5}\cdot\dfrac{25}{81}=\dfrac{65}{81}\)