(2x-5)^2024 + ( 3y+4)^26 ≤ 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
2
DT
22 tháng 6 2023
Vì : \(\left(2x-5\right)^{2022}\ge0\forall x,\left(3y+4\right)^{2024}\ge0\forall y\\ =>\left(2x-5\right)^{2022}+\left(3y+4\right)^{2024}\ge0\)
Do đó đề bài xảy ra khi và chỉ khi :
\(\left\{{}\begin{matrix}\left(2x-5\right)^{2022}=0\\\left(3y+4\right)^{2024}=0\end{matrix}\right.\\ =>\left(x;y\right)=\left(\dfrac{5}{2};-\dfrac{4}{3}\right)\)
NT
22 tháng 6 2023
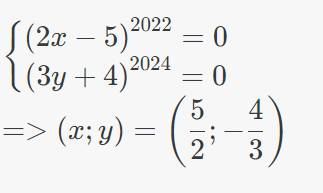Mình ko biết cách để làm ra đc kết quả này, có thể giải thích cụ thể hơn ko ạ?
AD
1
P
Phong
CTVHS
8 tháng 1 2024
\(\left(2x+4\right)^{2024}+\left(\left|3y-9\right|\right)^{2023}=0\) (*)
Ta có: \(\left(2x+4\right)^{2024}\ge0\forall x\) (vì có số mũ chẵn) (1)
\(\left(\left|3y-9\right|\right)^{2023}\ge0\forall y\) (vì giá trị tuyệt đối luôn ≥0) (2)
Từ (1) và (2) ta có:
\(\Rightarrow\left\{{}\begin{matrix}2x+4=0\\3y-9=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=-2\\y=3\end{matrix}\right.\)
Vậy: ...
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
14 tháng 8
\(\frac{x+2}{3}\) = \(\frac{y-5}{-4}\) = \(\frac{z+1}{1}\)
\(\frac{2x+4}{6}\) = \(\frac{3y-15}{-12}\) = \(\frac{z+1}{1}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{2x+4}{6}\) = \(\frac{3y-15}{-12}\) = \(\frac{z+1}{1}\) = \(\frac{2x+4-3y+15+z+1}{6+12+1}\) = \(\frac{2x-3y+z+\left(4+15+1\right)}{6+12+1}\)=\(\frac{2024+\left(19+1\right)}{18+1}\) = \(\frac{2024+20}{19}\) = \(\frac{2044}{19}\)
Em tự làm nốt nhá
P
3
25 tháng 7 2023
Vì `{(|x - 3y|^2023 >=0), (|y+4|^2024 >=0):} forall x, y`
Nên `{(x=3y), (y = -4):}`
`<=> {(x=-12), (y=-4):}`
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
22 tháng 6 2023
a,Nghiệm của (2\(x\) - 5)2022 là giá trị của \(x\) thỏa mãn
(2\(x\) - 5)2022 = 0
2\(x\) - 5 = 0
2\(x\) = 5
2\(x\) = 5:2
\(x\) = 2,5
b, Nghiệm của (3\(x\) + 4)2024 là giá trị của \(x\) thỏa mãn:
(3\(x\) + 4)2024 = 0
3\(x\) + 4 = 0
3\(x\) = -4
\(x\) = - 4 : 3
\(x\) = -\(\dfrac{4}{3}\)
PM
1
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 3 2022
A là giao điểm AB và AC nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}2x+y-5=0\\x-3y+1=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\) \(\Rightarrow A\left(2;1\right)\)
\(d\left(A;...\right)=\dfrac{\left|7.2-8.1+26\right|}{\sqrt{7^2+\left(-8\right)^2}}=\dfrac{32}{\sqrt{113}}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
17 tháng 12 2023
a, 7\(x\).(2\(x\) + 10) = 0
\(\left[{}\begin{matrix}x=0\\2x+10=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\2x=-10\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x=-10:2\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
Vậy \(x\in\){-5; 0}
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
17 tháng 12 2023
b, - 9\(x\) : (2\(x\) - 10) = 0
- 9\(x\) = 0
\(x\) = 0
c, (4 - \(x\)).(\(x\) + 3) = 0
\(\left[{}\begin{matrix}4-x=0\\x+3=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=4\\x=-3\end{matrix}\right.\)
Vậy \(x\in\) {-3; 4}
d, (\(x\) + 2023).(\(x\) - 2024) = 0
\(\left[{}\begin{matrix}x+2023=0\\x-2024=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-2023\\x=2024\end{matrix}\right.\)
Vậy \(x\) \(\in\) {-2023; 2024}
`(2x-5)^2024 + (3y+4)^26 <= 0`
Vì `(2x-5)^2024 >= 0 AA x`
`(3y+4)^26 >= 0 AA x`
`=>{(2x-5=0),(3y+4=0):}`
`<=>{(x=5/2),(x=-4/3):}`
Ta thấy: (2x - 5)2024≥ 0 ∀ x ∈ R
(3y + 4)26 ≥ 0 ∀ y ∈ R
=> (2x - 5)2024 + (3y + 4)26 ≥ 0
Mặt khác: (2x - 5)2024 + (3y + 4)26 ≤ 0
Suy ra: (2x - 5)2024 + (3y + 4)26 = 0
\(\Leftrightarrow\left\{{}\begin{matrix}2x-5=0\\3y+4=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{2}\\y=-\dfrac{4}{3}\end{matrix}\right.\)
Vậy...