Vật sáng AB đặt cách thấu kính một đoạn 20cm cho ảnh A'B' rõ nét trên màn M. Cho vật dịch chuyển một đoạn a = 2cm lại gần thấu kính ta phải dịch chuyển màn M một đoạn b để thu được ảnh A''B'' rõ nét trên màn. Biết A''B'' = \(\dfrac{5}{3}\) A'B'. Tính tiêu cự của thấu kính và độ dịch chuyển b
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
3 tháng 11 2017
Chọn đáp án C.
Thấu kính hội tụ cho ảnh cao bằng nửa vật → ảnh thật → ngược chiều với vật => k = - 0,5.
⇒ − 0 , 5 = f f − d ⇒ d = 60 c m ⇒ − 0 , 5 = − d ' d ⇒ d ' = 30 c m .
⇒ a = d + d ' = 90 ( c m ) .
29 tháng 4 2021
Sơ đồ tạo ảnh
AB → A’B’
d d’
Công thức thấu kính: 
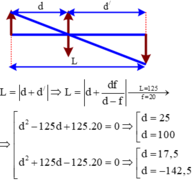
Gọi khoảng cách từ vật tới ảnh là L ⇒ |d’ + d| = L.
Vật thật ⇒ d > 0
L = 125cm
∗ Trường hợp 1: A’B’ là ảnh thật → d’ > 0
→ L = d’ + d =125cm (2)
Từ (1) và (2) ta có:
Giải phương trình lấy nghiệm d1 > 0 ta được: d1 = 17,54 cm
∗ Trường hợp 2
d’ + d = - 125cm (trường hợp này thì ảnh A’B’ là ảnh ảo) (3)
Từ (1) và (3) ta có:
Giải phương trình lấy nghiệm d > 0 ta được: d = 25cm hoặc d = 100cm
VT
9 tháng 11 2018
Sơ đồ tạo ảnh:
Áp dụng công thức về vị trí ảnh – vật:
Như vậy k > 0 nên ảnh cùng chiều với vật cao bằng một phần ba vật.
VT
29 tháng 9 2019
Đáp án cần chọn là: A
Vì ảnh hứng trên màn nên: L = d + d ' = 90 c m (1)
+ Theo công thức thấu kính, ta có: 1 f = 1 d + 1 d ' → d ' = d f d − f (2)
Thế (2) vào (1), ta được:
d + d f d − f = L ↔ d 2 − L d + L f = 0
↔ d 2 − 90 d + 90.20 = 0
→ d = 30 c m d = 60 c m
VT
29 tháng 9 2019
Đáp án cần chọn là: B
1 f = 1 d + 1 d ' → 1 − 20 = 1 20 + 1 d ' → d ' = − 10 c m
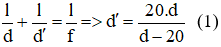
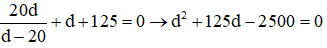
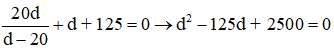
\(\dfrac{1}{f}=\dfrac{1}{d_1}+\dfrac{1}{d_1'};\left\{{}\begin{matrix}d_2=d_1-2\\d_2'=d_1'+b\end{matrix}\right.;\dfrac{A"B"}{A'B'}=\dfrac{5}{3}\Leftrightarrow\dfrac{d_2'.d_1}{d_1'.d_2}=\dfrac{5}{3}\)
\(\Rightarrow\dfrac{\left(d_1'+b\right).d_1}{d_1'.\left(d_1-2\right)}=\dfrac{5}{3}\)\(\Leftrightarrow\dfrac{20\left(d_1'+b\right)}{d_1'\left(20-2\right)}=\dfrac{5}{3}\)
\(\dfrac{A"B"}{A'B'}=\dfrac{5}{3}\Leftrightarrow\dfrac{k_2}{k_1}=\dfrac{f-d_1}{f-d_2}=\dfrac{5}{3}\Leftrightarrow\dfrac{f-20}{f-20+2}=\dfrac{5}{3}\Rightarrow f=....\)
\(\Rightarrow d_1'=\dfrac{fd_1}{d_1-f}=...;\dfrac{20\left(d_1'+b\right)}{18d_1'}=\dfrac{5}{3}\Rightarrow b=...\)
30cm