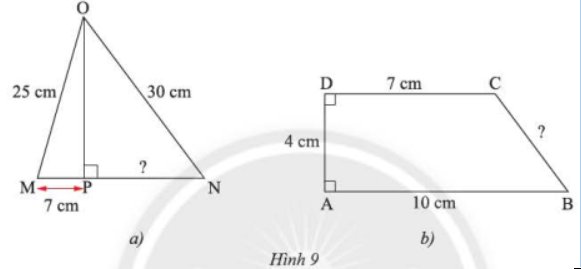
Tính các độ dài \(PN\) và \(BC\) trong Hình 9.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NM
1
J
15 tháng 5 2021
a)Độ dài đường gấp khúc ABCD là :
AB + BC + CD + AD = 4 + 7 + 3 + 9 = 23 (cm)
b) vì 23 > 9
nên độ dài đường gấp khúc ABCD lớn hơn độ dài đoạn thẳng AD
15 tháng 5 2021
a) Độ dài đường gấp khúc ABCD là:
4+7+3+9=23(cm)
b) Vì 23cm > 9cm
=> Độ dài đường gấp khúc ABCD lớn hơn độ dài đoạn thẳng AD.
22 tháng 2 2022
a) AB = CD = PQ = MN
AD = BC = NP = MQ
AM = BN = CP = DQ
b) Diện tích mặt đáy MNPQ là: 6 x 3 = 18 (cm2)
Diện tích mặt bên ABNM là: 6 x 4 = 24 (cm2)
Diện tích mặt bên BCPN là: 3 x 4 = 12 (cm2).
VN
16 tháng 2 2017
30 8cm A B C
Tam giac ABC la nua tam giac deu.
Chieu cao hinh thang la AC=8/2=4 (cm)
Dien h hinh thang la S=\(\frac{\left(7+9\right)}{2}4\)=32 (cm vuong)
16 tháng 2 2017
Võ Nhật Lê sai rồi nếu tam giác ABC là nữ tam giác đêu thì AB=2BC mới đúng chứ ko phải là AB=2AC
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
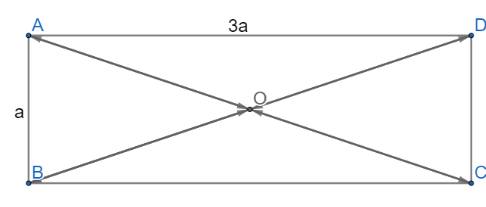
a) Ta có:
\(AC = BD = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {{\left( {3a} \right)}^2}} = a\sqrt {10} \)
+) \(\left| {\overrightarrow {AC} } \right| = AC = a\sqrt {10} \)
+) \(\left| {\overrightarrow {BD} } \right| = BD = a\sqrt {10} \)
b) O là giao điểm của hai đường chéo nên ta có:
\(AO = OC = BO = OD = \frac{{a\sqrt {10} }}{2}\)
Dựa vào hình vẽ ta thấy AO và CO cùng nằm trên một đường thẳng; BO và DO cùng nằm trên một đường thẳng
Suy ra các cặp vectơ đối nhau và có độ dài bằng \(\frac{{a\sqrt {10} }}{2}\) là:
\(\overrightarrow {OA} \) và \(\overrightarrow {OC} \); \(\overrightarrow {AO} \) và \(\overrightarrow {CO} \); \(\overrightarrow {OB} \) và \(\overrightarrow {OD} \); \(\overrightarrow {BO} \) và \(\overrightarrow {DO} \)
a: QP=căn 25^2-7^2=24cm
PN=căn 30^2-24^2=18cm
b: Kẻ CH vuông góc AB
Xét tứ giác ADCH có
góc ADC=góc A=góc CHA=90 độ
=>ADCH là hcn
=>AH=CD=7cm
=>BH=3cm và CH=AD=4cm
=>BC=căn 3^2+4^2=5cm