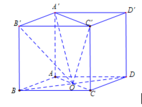
Cho hình hộp \(ABCD.A'B'C'D'\). Gọi \({G_1}\) và \({G_2}\) lần lượt là trọng tâm của hai tam giác \(BDA'\) và \(B'D'C\). Chứng minh \({G_1}\) và \({G_2}\) chia đoạn \(AC\) thành ba phần bằng nhau.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


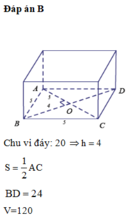
Đáp án là C.
Ta có: V O . A , B , C , = 1 2 V O . A , B , C , D , ; V O . A , B , C , D , 1 3 V A B C D . A , B , C , D ,
V O . A , B , C , = 1 6 V A B C D . A , B , C , D , ⇒ V O . A , B , C , V A B C D . A , B , C , D = 1 6


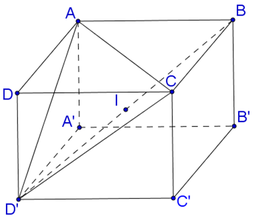
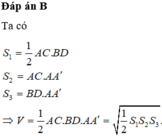

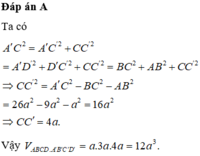
Gọi \(O = AC \cap B{\rm{D}},O' = A'C' \cap B'{\rm{D}}',I = AC' \cap A'C\)
Vì \(AA'\parallel CC',AA' = CC'\) theo tính chất hình hộp nên \(AA'C'C\) là hình bình hành \( \Rightarrow I\) là trung điểm của \(AC'\) và \(A'C\).
Ta có: \({G_1}\) là trọng tâm của tam giác \(BDA' \Rightarrow \frac{{A'{G_1}}}{{A'O}} = \frac{2}{3}\)
Tam giác \(AA'C\) có \(\frac{{A'{G_1}}}{{A'O}} = \frac{2}{3}\) nên \({G_1}\) là trọng tâm của tam giác \(AA'C\)
Mà \(I\) là trung điểm của \(A'C\) nên \(\frac{{A{G_1}}}{{AI}} = \frac{2}{3} \Rightarrow A{G_1} = \frac{2}{3}AI\)
Mà \(AI = \frac{1}{2}AC'\)
\( \Rightarrow A{G_1} = \frac{1}{3}AC'\left( 1 \right)\)
Ta có: \({G_2}\) là trọng tâm của tam giác \(B'D'C \Rightarrow \frac{{C{G_2}}}{{CO'}} = \frac{2}{3}\)
Tam giác \(ACC'\) có \(\frac{{C{G_2}}}{{CO'}} = \frac{2}{3}\) nên \({G_2}\) là trọng tâm của tam giác \(ACC'\)
Mà \(I\) là trung điểm của \(AC'\) nên \(\frac{{C'{G_2}}}{{C'I}} = \frac{2}{3} \Rightarrow C'{G_2} = \frac{2}{3}C'I\)
Mà \(C'I = \frac{1}{2}AC'\)
\( \Rightarrow C'{G_2} = \frac{1}{3}AC'\left( 2 \right)\)
Từ (1) và (2) suy ra \({G_1}\) và \({G_2}\) chia đoạn \(AC\) thành ba phần bằng nhau.