làm câu a) ạ, lát e đưa câu b
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 8 2023
a) Các vị trí so le trong, và đồng vị với \(\widehat{mAB}\) là:
\(\widehat{B_1};\widehat{APQ};\widehat{nPA}\)
b) Ta có: \(\widehat{B_1}=\widehat{mAB}=50^o\) (hai góc so le trong)
Mà: \(\widehat{B_1}+\widehat{B_2}=180^o\Rightarrow\widehat{B_2}=180^o-50^o=130^o\)
c) Ta có: \(\widehat{mAB}+\widehat{A_1}=180^o\Rightarrow\widehat{A_1}=180^o-\widehat{mAB}=180^o-50^o=130^o\)
Mà: \(\widehat{mAB}=\widehat{A_2}=50^o\)(hai góc đối đỉnh)
d) Ta có:
\(\widehat{APQ}+\widehat{PQB}=180^o\)
\(\Rightarrow\widehat{PQB}=180^o-\widehat{APQ}=180^o-110^o=70^o\)
TN
1
3 tháng 8 2023
a: góc yAt'=180 độ-60 độ=120 độ
góc yAt'=góc yOx
mà hai góc này đồng vị
nên At'//Ox
b: góc mOA=góc xOy/2=60 độ
góc nAO=góc OAt/2=60 độ
=>góc mOA=góc nAO
=>Om//An
1 tháng 8 2023
\(0,\left(37\right)+0,\left(62\right)\)
\(=\dfrac{37}{99}+\dfrac{62}{99}\)
\(=\dfrac{37+62}{99}\)
\(=\dfrac{99}{99}\)
\(=1\)
QT
Quoc Tran Anh Le
Giáo viên
1 tháng 8 2023
Để chứng tỏ một bài, em hãy giải thích tính chất của hai số trong biểu thức nhé: đó là những số thập phân vô hạn tuần hoàn, từ đó chúng ta mới biểu diễn chúng dưới dạng phân số quy tắc.
TN
1
1 tháng 8 2023
a: \(A=\dfrac{3n^2+3n}{12n}=\dfrac{3n\left(n+1\right)}{3n\cdot4}=\dfrac{n+1}{4}\)
Vì 4=2^2 ko có thừa số nguyên tố nào khác 2 và 5
nên \(A=\dfrac{n+1}{4}\) viết được dưới dạng số thập phân hữu hạn
4 tháng 8 2023
góc xOz=góc yOz=90/2=45 độ
Bm//Oz
=>góc mBO+góc BOz=180 độ
=>góc mBO=135 độ
Cn//Oz
=>góc nCy=góc zOy(hai góc đồng vị)
=>góc nCy=45 độ
6 tháng 8 2023
a: x<a<y
=>102,39...<a<103,02...
=>a=103; a=103,01; a=103,015
b: x<a<y
=>-0,41...<a<0,41...
=>a=0; a=0,2; a=0,3
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
6 tháng 8 2023
a, a = 102,4 hoặc a=103 hoặc a= 103,01
b, a=0,4 hoặc a=0 hoặc a=-0,1
13 tháng 10 2021
Bạn chỉ cần áp dụng cái phân tích đa thức thành nhân tử bằng phương pháo đặt nhân tử chung là ra rồi
NT
5
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 10 2021
b.
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=-\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=-\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{3}=\dfrac{2\pi}{3}+k2\pi\\x+\dfrac{\pi}{3}=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=-\pi+k2\pi\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 10 2021
c.
\(\Leftrightarrow\dfrac{3}{5}sinx-\dfrac{4}{5}cosx=1\)
Đặt \(\dfrac{3}{5}=cosa\) với \(a\in\left(0;\dfrac{\pi}{2}\right)\Rightarrow\dfrac{4}{5}=sina\)
Pt trở thành:
\(sinx.cosa-cosx.sina=1\)
\(\Leftrightarrow sin\left(x-a\right)=1\)
\(\Leftrightarrow x-a=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=a+\dfrac{\pi}{2}+k2\pi\)
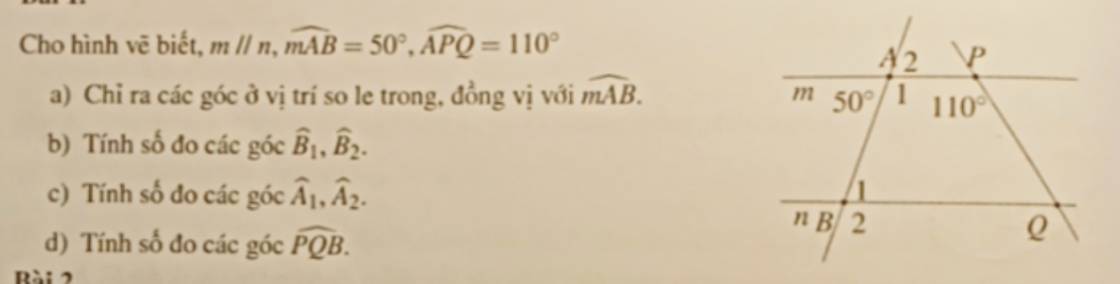
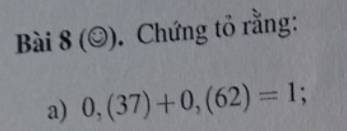
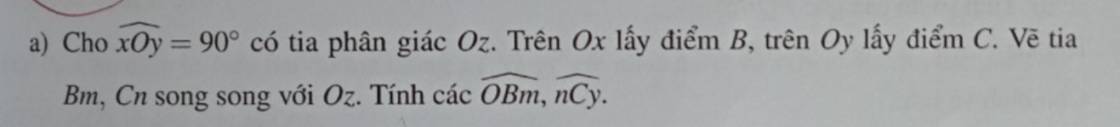
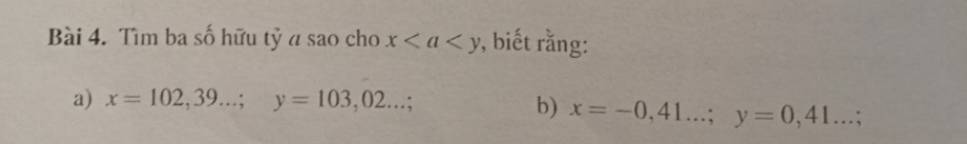
a
Hai góc \( \widehat{ AOM}, \widehat{BON }\) không phải 2 góc đối đỉnh.
Vì \(\widehat{ AOM} \)và \(\widehat{BON } \)chỉ có một cặp cạnh là hai tia đối nhau, cặp cạnh còn lại không đối nhau.