Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(BD=\sqrt{16^2+12^2}=20\left(cm\right)\)
AH=12*16/20=192/20=9,6cm
MH=9,6-4=5,6cm
DH=12^2/20=144/20=7,2cm
=>HN=7,2-3=4,2cm
=>HN/HD=HM/HA
=>MN//AD
=>MN vuông góc AB
Xét ΔANB có
AH,NM là đường cao
AH cắt NM tại M
=>M là trực tâm
=>BM vuông góc AN
Áp dụng định nghĩa và giả thiết của hình vuông ABCD ta được:
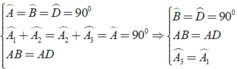
⇒ Δ ABM = Δ ADN( g - c - g )
Do đó AM = AN (cặp cạnh tương ứng bằng nhau)
a: XétΔMAD vuông tại A và ΔNBA vuông tại B có
MA=NB
AD=BA
Do đó: ΔMAD=ΔNBA
=>DM=AN và \(\widehat{AMD}=\widehat{BNA}\)
=>\(\widehat{AMD}+\widehat{MAN}=90^0\)
=>DM vuông góc AN
b: AM+MB=AB
BN+NC=BC
mà AM=BN và AB=BC
nên MB=NC
Xét ΔMBC vuông tại B và ΔNCD vuông tại C có
MB=NC
BC=CD
Do đó: ΔMBC=ΔNCD
=>\(\widehat{BMC}=\widehat{CND}\)
=>\(\widehat{CND}+\widehat{NCM}=90^0\)
=>DN vuông góc MC
Xét ΔDMN có
CM,NA là đường cao
CM cắt NA tại X
Do đó: X là trực tâm
=>DX vuông góc MN
a: XétΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN
Suy ra AM=AN
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{HAB}=\widehat{KAC}\)
Do đó: ΔAHB=ΔAKC
Suy ra: BH=CK
làm tương tự
Cho hình vuông ABCD. Gọi O là giao điểm của hai đường chéo AC và BD, M là trung điểm của OB, N là trung điểm của CD.
a, Chứng minh: +góc AMN vuông.
+A, M, N, D cùng thuộc một đường tròn, xác định tâm của nó.
+ AN>MD
b, Trên AB, AD thứ tự lấy I, K sao AI=Ak. Kẻ AP vuông góc DI, cắt BC tại Q. Chứng minh 5 điểm C, D, K, P, Q cùng nằm trên một đường tròn
Bài làm
Từ M hạ ME vuông góc AD,MF vuông góc DC (ME//AB, MF//BC) , nối MA và MN ta có DM = 3/4.DB => AE = CF = 1/4 AD ( AD = DC= AB = BC cạnh hình vuông)
ME = MF = 3/4.AB, NC = 1/2.DC và CF = 1/4 DC => NF = 1/4 DC
=> tam giác vuông AEM = tam giác vuông NFM ( hai cặp cạnh góc vuông bằng nhau đôi một)
=>góc AME = góc NMF mà góc NMF + góc EMN = 90 độ => góc AME + góc EMN = 90 độ
=> góc AMN = 90 độ (điều phải cm)
Gọi I là trung điểm AN, do tam giác ADN vuông tại D =>ID= IA = IN (trung tuyến thuộc cạnh huyền bằng 1/2 cạnh huyền) , tương tự có tam giác AMN vuông tại M => IM = IA = IN
=> 4 điểm A, D, N, M cách đều I => A, M, N, D cùng thuộc một đường tròn tâm là trung điểm I của đoạn AN
tam giác vuông cân DEM có DM^2 = 2.ME^2
tam giác vuông cân AMN có AN^2 = 2.MA^2 mà MA > ME
=> AN^2 > DM^2 => AN > DM (điều phải cm)
b, Trên AB, AD thứ tự lấy I, K sao AI=Ak. Kẻ AP vuông góc DI, cắt BC tại Q. Chứng minh 5 điểm C, D, K, P, Q cùng nằm trên một đường tròn
góc DPQ = 90 độ (theo cách dựng AP vuông góc DI)
và góc DCQ = 90 độ (gt ABCD là hình vuông) nên D, P, C, Q thuộc đường tròn đường kính DQ.
ta sẽ c/m K thuộc đường tròn đường kính DQ.nghĩa là góc DKQ = 90 độ
xét tứ giác IPQB có góc P và B vuông => góc PQB + góc PIB = 180 độ
mà góc góc PIB + góc PIA = 180 độ =>góc PIA =góc PQB => góc DIA = góc AQB
xét 2 tam giác vuông DAI và ABQ có AD = AB và góc DIA = góc AQB
=> tam giác DAI = tam giác ABQ ( cạnh góc vuông, góc nhọn) => AK = BQ => KQ//AB
=> góc DKQ = 90 độ => K thuộc đường tròn đường kính DQ.
=> 5 điểm C, D, K, P, Q cùng nằm trên một đường tròn ( điều phải c/m)
AH vuông góc DM
=>góc MAH=góc MDA
Xét ΔABP vuông tại B và ΔDAM vuông tại A có
AB=AD
góc MAH=góc MDA
=>ΔABP=ΔDAM
=>BP=AM=AN
mà BC=AD
nên PC=ND
=>PCND là hình chữ nhật
=>P,C,D,N cùng nằm trên đường tròn đường kính DP
mà H nằm trên đường tròn đường kính DP(góc DHP=90 độ)
nên C,D,N,H,P cùng thuộc 1 đường tròn
Để chứng minh rằng \(C I\) vuông góc với \(A N\), ta sẽ sử dụng lý thuyết hình học phẳng, đặc biệt là các tính chất của các đường chéo, các đường phân giác và các tam giác vuông.
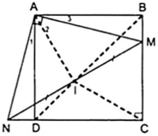
Cho hình vuông \(A B C D\), trên cạnh \(B C\) lấy điểm \(M\), \(A M\) cắt đường thẳng \(C D\) tại điểm \(N\). Kéo dài \(D M\) cắt \(B N\) tại điểm \(I\). Chứng minh rằng \(C I\) vuông góc với \(A N\).
Để chứng minh các đường vuông góc, chúng ta có thể sử dụng định lý Menelaus cho tam giác \(A N D\) với các điểm cắt tạo ra bởi các đoạn thẳng liên quan. Cụ thể, định lý Menelaus nói rằng nếu một đường thẳng cắt ba cạnh (hoặc ba đường thẳng kéo dài) của một tam giác, thì các tỉ số đoạn cắt thỏa mãn một điều kiện nhất định.
Trong trường hợp này, ta có thể áp dụng định lý Menelaus cho tam giác \(A N D\) với các điểm cắt \(I\), \(M\), và \(B\).
Vì \(A B C D\) là hình vuông, các góc của nó đều là góc vuông (\(90^{\circ}\)), và các cạnh của nó bằng nhau. Điều này giúp chúng ta suy ra các quan hệ giữa các đoạn thẳng trong hình vuông.
Để chứng minh rằng \(C I\) vuông góc với \(A N\), ta cần chỉ ra rằng các vectơ \(\overset{\rightarrow}{C I}\)và \(\overset{\rightarrow}{A N}\)có tích vô hướng bằng 0, tức là:
\(\overset{\rightarrow}{C I} \cdot \overset{\rightarrow}{A N} = 0\)
Điều này có thể thực hiện bằng cách sử dụng các tính chất vectơ của các đoạn thẳng trong hình vuông và các đường cắt.
Qua các bước phân tích trên, ta có thể chứng minh rằng \(C I\) vuông góc với \(A N\), bằng cách sử dụng các tính chất của các đoạn thẳng trong hình vuông và các định lý liên quan đến giao điểm.
a: Xét ΔABM vuông tại B và ΔADN vuông tại D có
AB=AD
góc BAM=góc DAN
=>ΔABM=ΔADN
=>AM=AN
=>ΔAMN vuông cân tại A
b: 1/AM^2+1/AE^2
=1/AN^2+1/AE^2
=1/AD^2 ko đổi