trong mặt phẳng tọa độ cho 2 điểm A(4;-1);B(-2;5). Viết phương trình đường tròn đường kính AB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 3 2018
Chọn D.
Gọi điểm M có tọa độ là ( x; y)
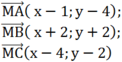
MA2 + 2MB2 + 3MC2
= (x - 1)2 + (y - 4)2 + 2[ (x + 2)2 + (y + 2)2] + 3[ (x - 4)2 + (y - 2)2]
= 6x2-18x + 6y2 + 93 = 1,5. (2x - 3)2 + 6(y - 1)2 + 147/2 ≥ 147/2
Dấu “=” xảy ra khi x = 1,5 và y = 1
Vậy tọa độ điểm M cần tìm là ( 1,5; 1).
CM
19 tháng 8 2018
Ta có C ∈ O x nên C(c; 0) và C A → = − 2 − c ; 4 C B → = 8 − c ; 4 .
Tam giác ABC vuông tại C nên C A → . C B → = 0 ⇔ − 2 − c . 8 − c + 4.4 = 0
⇔ c 2 − 6 c = 0 ⇔ c = 6 → C 6 ; 0 c = 0 → C 0 ; 0 .
Chọn B.
CM
26 tháng 12 2018
Ta có C ∈ O x nên C(c, 0) và C A → = − 2 − c ; 4 C B → = 8 − c ; 4 .
Tam giác ABC vuông tại C nên C A → . C B → = 0 ⇔ − 2 − c . 8 − c + 4.4 = 0
⇔ c 2 − 6 c = 0 ⇔ c = 6 → C 6 ; 0 c = 0 → C 0 ; 0 .
Chọn B.
CM
5 tháng 3 2017
Gọi C(x, y).
Ta có B A → = 1 ; 3 B C → = x − 1 ; y − 1 .
Tam giác ABC vuông cân tại B:
⇔ B A → . B C → = 0 B A = B C ⇔ 1. x − 1 + 3. y − 1 = 0 1 2 + 3 2 = x − 1 2 + y − 1 2
⇔ x = 4 − 3 y 10 y 2 − 20 y = 0 ⇔ y = 0 x = 4 hay y = 2 x = − 2 .
Chọn C.
CM
8 tháng 2 2018
Ta có C ∈ O x nên C(x, 0) và A C → = x − 1 ; − 3 B C → = x − 4 ; − 2 .
Do C A = C B ⇔ C A 2 = C B 2 .
⇔ x − 1 2 + − 3 2 = x − 4 2 + − 2 2 ⇔ x 2 − 2 x + 1 + 9 = x 2 − 8 x + 16 + 4 ⇔ 6 x = 10 ⇔ x = 5 3 ⇒ C 5 3 ; 0
Chọn B.
12 tháng 1 2023
a: A(2;4); B(1;0); C(2;2)
vecto AB=(-1;-4)
vecto DC=(2-x;2-y)
Vì ABCD là hình bình hành nên vecto AB=vecto DC
=>2-x=-1 và 2-y=-4
=>x=3 và y=6
c: N đối xứng B qua C
=>x+1=4 và y+0=4
=>x=3 và y=4
Tọa độ tâm I là:
x=(4-2)/2=1 và y=(-1+5)/2=2
I(1;2); A(4;-1)
\(IA=\sqrt{\left(4-1\right)^2+\left(-1-2\right)^2}=3\sqrt{2}\)
=>Phương trình đường tròn là:
(x-1)^2+(y-2)^2=18